Bài 3 trang 97 Toán 9 Tập 1 Chân trời sáng tạo

Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

Giải Toán 9 Bài 3: Góc ở tâm, góc nội tiếp - Chân trời sáng tạo

Bài 3 trang 97 Toán 9 Tập 1: Dây cung AB chia đường tròn (O) thành hai cung. Cung lớn có số đo bằng ba lần cung nhỏ.

a) Tính số đo mỗi cung.

b) Chứng minh khoảng cách OH từ tâm O đến dây cung AB có độ dài bằng $\frac{A B}{2} .$

Lời giải:

Bài 3 trang 97 Toán 9 Tập 1 Chân trời sáng tạo

a) Gọi $\overset{⏜}{A m B}$ và $\overset{⏜}{A n B}$ lần lượt là cung lớn và cung nhỏ AB.

Theo bài, ta có: $s đ \overset{⏜}{A m B} = 3 s đ \overset{⏜}{A n B} .$

Mà $s đ \overset{⏜}{A m B} + \overset{⏜}{A n B} = 360 °$

Nên $s đ \overset{⏜}{A n B} + 3 s đ \overset{⏜}{A n B} = 360 °$

Hay $4 s đ \overset{⏜}{A n B} = 360 °,$ suy ra $s đ \overset{⏜}{A n B} = 90 ° .$

Do đó $s đ \overset{⏜}{A m B} = 3 s đ \overset{⏜}{A n B} = 3 \cdot 90 ° = 270 ° .$

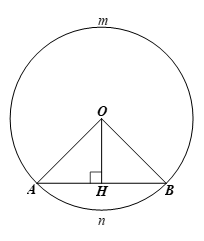
b) Xét ∆OAB có OA = OB (cùng bằng bán kính của đường tròn (O)) nên ∆OAB cân tại O.

Do đó đường cao OH đồng thời là đường trung tuyến của tam giác.

Lại có $s đ \overset{⏜}{A n B} = 90 °$ (câu a) nên $\hat{A O B} = 90 ° .$

Khi đó ∆OAB vuông tại O có OH là đường trung tuyến ứng với cạnh huyền AB nên $O H = \frac{A B}{2} .$

Lời giải bài tập Toán 9 Bài 3: Góc ở tâm, góc nội tiếp hay, chi tiết khác: