Bài 14 trang 105 Toán 9 Tập 1 Chân trời sáng tạo
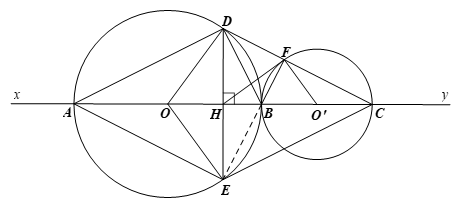
Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
Giải Toán 9 Bài tập cuối chương 5 - Chân trời sáng tạo
Bài 14 trang 105 Toán 9 Tập 1: Trên đường thẳng xy, lấy lần lượt ba điểm A, B, C sao cho AB > BC. Vẽ đường tròn (O) đường kính AB và đường tròn (O’) đường kính BC.
a) Chứng minh rằng hai đường tròn (O) và (O’) tiếp xúc ngoài tại B.
b) Gọi H là trung điểm của AC. Vẽ dây DE của (O) vuông góc với AC tại H. Chứng minh tứ giác ADCE là hình thoi.
c) DC cắt đường tròn (O’) tại F. Chứng minh rằng ba điểm F, B, E thẳng hàng.
d) Chứng minh rằng HF là tiếp tuyến của đường tròn (O’).
Lời giải:
a) Ta có OO’ = OB + BO’ nên đường tròn (O) và (O’) tiếp xúc ngoài tại B.
b) Xét ∆ODE có OD = OE (cùng là bán kính của đường tròn (O) đường kính AB) nên ∆ODE cân tại O. Do đó đường cao OH đồng thời là đường trung tuyến của tam giác hay H là trung điểm của DE.
Xét tứ giác ADCE có hai đường chéo AC và DE cắt nhau tại trung điểm H của mỗi đường nên ADCE là hình bình hành.
Lại có DE ⊥ AC tại H nên hình bình hành ADCE là hình thoi.
c) Xét đường tròn (O) có AB là đường kính, là góc nội tiếp chắn nửa đường tròn nên do đó AD ⊥ DB.
Lại có AD // CE (do ADCE là hình thoi) nên DB ⊥ CE.
Xét ∆CDE có DB, CH là hai đường cao của tam giác cắt nhau tại B (do DB ⊥ CE và CH ⊥ DE) nên B là trực tâm của ∆CDE. Suy ra EF ⊥ CD. (1)
Xét đường tròn (O’) có BC là đường kính, là góc nội tiếp chắn nửa đường tròn nên do đó BF ⊥ CD. (2)
Từ (1) và (2) ta có EF, BF là hai đường thẳng cùng đi qua điểm F và vuông góc với CD nên là hai đường thẳng trùng nhau, hay ba điểm E, B, F thẳng hàng.
d) Vì BF ⊥ CD nên ∆DEF vuông tại F có FH là đường trung tuyến ứng với cạnh huyền nên mà H là trung điểm của DE nên do đó FH = HE.
Xét ∆HEF có FH = HE nên ∆HEF cân tại H. Do đó (hai góc ở đáy bằng nhau).
Xét ∆O’BF có O’B = O’F (cùng là bán kính của đường tròn (O’) đường kính BC) nên ∆O’BF cân tại O’. Suy ra (hai góc ở đáy bằng nhau).
Mà (đối đỉnh) nên
Ta có: (do ∆HBE vuông tại H).
Hay nên HF ⊥ O’F tại F.
Xét đường tròn (O’) có HF ⊥ O’F tại F thuộc đường tròn nên HF là tiếp tuyến của đường tròn (O’).
Lời giải bài tập Toán 9 Bài tập cuối chương 5 hay, chi tiết khác:
Bài 4 trang 103 Toán 9 Tập 1: Hình nào dưới đây biểu diễn góc nội tiếp? ....
Bài 5 trang 103 Toán 9 Tập 1: Góc nội tiếp chắn nửa đường tròn có số đo là ....
Bài 8 trang 104 Toán 9 Tập 1: Trong một đường tròn, khẳng định nào sau đây là sai? ....
Bài 9 trang 104 Toán 9 Tập 1: Hình quạt tròn bán kính R, ứng với cung 90° có diện tích bằng ....