Bài 2 trang 82 Toán 9 Tập 1 Chân trời sáng tạo

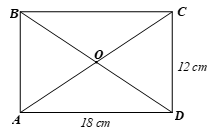
Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Giải Toán 9 Bài 1: Đường tròn - Chân trời sáng tạo

Bài 2 trang 82 Toán 9 Tập 1: Cho hình chữ nhật ABCD có AD = 18 cm và CD = 12 cm. Chứng minh rằng bốn điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

⦁ Vì ABCD là hình chữ nhật nên AC = BD. (1)

Gọi O là giao điểm của hai đường chéo AC, BD của hình chữ nhật.

Khi đó, O là trung điểm của AC và BD (tính chất hình chữ nhật) nên $OA=OC=\frac{1}{2}AC;$ $OB=OD=\frac{1}{2}BD.$(2)

Từ (1) và (2) ta có $OA=OC=OB=OD=\frac{1}{2}AC=\frac{1}{2}BD.$

Vậy bốn điểm A, B, C, D cùng thuộc một đường tròn đường kính AC, BD.

⦁ Vì ABCD là hình chữ nhật nên $\widehat{ADC}=90°.$

Xét ∆ADC vuông tại D, theo định lí Pythagore, ta có:

AC² = AD² + DC² = 18² + 12² = 468.

Do đó $AC=\sqrt{468}=\sqrt{6^2\cdot 13}=6\sqrt{13}\text{ (cm).}$

Vậy bán kính đường tròn đi qua bốn điểm A, B, C, D là $\frac{1}{2}AC=\frac{1}{2}\cdot 6\sqrt{13}=3\sqrt{13}\text{ (cm).}$

Lời giải bài tập Toán 9 Bài 1: Đường tròn hay, chi tiết khác:

• Khởi động trang 75 Toán 9 Tập 1: Hãy chỉ ra các bộ phận có dạng đường tròn của chiếc xe đạp trong hình dưới đây ....

• Khám phá 1 trang 75 Toán 9 Tập 1: Mở một chiếc compa sao cho hai đầu compa cách nhau một khoảng R cho trước ....

• Khám phá 2 trang 76 Toán 9 Tập 1: a) Cho đường tròn (O; R). i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ ....

• Thực hành 1 trang 77 Toán 9 Tập 1: Xác định tâm đối xứng và trục đối xứng của bánh xe trong Hình 7. Giải thích cách làm ....

• Vận dụng 1 trang 77 Toán 9 Tập 1: Nêu cách chia một cái bánh có dạng hình tròn tâm O (Hình 8) thành hai phần bằng nhau ....

• Khám phá 3 trang 77 Toán 9 Tập 1: Trên đường tròn (O; R), lấy bốn điểm A, B, M, N sao cho AB đi qua O và MN không đi qua O (Hình 9) ....

• Thực hành 2 trang 78 Toán 9 Tập 1: Cho đường tròn (I) có các dây cung AB, CD, EF. Cho biết AB và CD đi qua tâm I ....

• Vận dụng 2 trang 78 Toán 9 Tập 1: Bạn Mai căng ba đoạn chỉ AB, CD, EF có độ dài lần lượt là 16 cm, 14 cm và 20 cm ....

• Khám phá 4 trang 78 Toán 9 Tập 1: Tìm số điểm chung của hai đường tròn (O) và (O’) trong mỗi trường hợp sau ....

• Khám phá 5 trang 79 Toán 9 Tập 1: Cho hai đường tròn phân biệt (O; R) và (O’; R’) với R ≥ R’. Hãy so sánh OO’ với R + R’ ....

• Thực hành 3 trang 80 Toán 9 Tập 1: Xác định vị trí tương đối giữa hai đường tròn (I; R) và (J; R’) trong mỗi trường hợp sau ....

• Vận dụng 3 trang 81 Toán 9 Tập 1: Mô tả vị trí tương đối giữa mỗi cặp đường tròn trong hình chụp bộ cồng chiêng Tây Nguyên trong Hình 18 ....

• Vận dụng 4 trang 81 Toán 9 Tập 1: Dùng compa đo bán kính và vẽ lại các hình trong Hình 19 ....

• Bài 1 trang 82 Toán 9 Tập 1: Cho đường tròn (O), bán kính 5 cm và bốn điểm A, B, C, D thoả mãn OA = 3 cm ....

• Bài 3 trang 82 Toán 9 Tập 1: Cho tam giác ABC có hai đường cao BB’ và CC’. Gọi O là trung điểm của BC ....

• Bài 4 trang 82 Toán 9 Tập 1: Cho tứ giác ABCD có $\widehat{\text{B}}=\widehat{\text{D}}=90°.$ ....

• Bài 5 trang 82 Toán 9 Tập 1: Cho hai đường tròn (O; 2 cm) và (A; 2 cm) cắt nhau tại C, D, điểm A nằm trên đường tròn tâm O (Hình 20) ....

• Bài 6 trang 82 Toán 9 Tập 1: Cho hai đường tròn (A; 6 cm) và (B; 4 cm) cắt nhau tại C và D, AB = 8 cm ....

• Bài 7 trang 82 Toán 9 Tập 1: Xác định vị trí tương đối của (O; R) và (O’; R’) trong mỗi trường hợp sau ....