Khám phá 2 trang 76 Toán 9 Tập 1 Chân trời sáng tạo
Giải Toán 9 Bài 1: Đường tròn - Chân trời sáng tạo
Khám phá 2 trang 76 Toán 9 Tập 1:
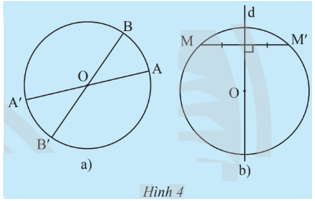
a) Cho đường tròn (O; R).
i) Lấy điểm A nằm trên đường tròn. Vẽ đường thẳng AO cắt đường tròn tại điểm A’ khác A. Giải thích tại sao O là trung điểm của đoạn thẳng AA’.
ii) Lấy điểm B khác A thuộc đường tròn (O; R). Tìm điểm B’ sao cho O là trung điểm của đoạn thẳng BB’. Điểm B’ có thuộc đường tròn (O; R) không? Giải thích.
b) Cho đường tròn (O; R), d là đường thẳng đi qua tâm O. Lấy điểm M nằm trên đường tròn. Vẽ điểm M’ sao cho d là đường trung trực của đoạn thẳng MM’ (khi M thuộc d thì lấy M’ trùng với M). Điểm M’ có thuộc đường tròn (O; R) không? Giải thích.
Lời giải:
a)
i) Vì hai điểm A, A’ cùng nằm trên đường tròn (O; R) nên OA = OA’ = R.
Mà điểm O nằm giữa hai điểm A và A’ nên O là trung điểm của AA’.
ii) Vì O là trung điểm của BB’ nên OB = OB’ (tính chất trung điểm một đoạn thẳng).
Lại có điểm B thuộc đường tròn (O; R) nên OB = R. Do đó OB’ = R.
Vậy điểm B’ thuộc đường tròn (O; R).
b) Nối OM, OM’.
⦁ Trường hợp 1: Điểm M thuộc d thì điểm M’ trùng điểm M.
Mà điểm M thuộc đường tròn (O; R) nên điểm M’ thuộc đường tròn (O; R).
⦁ Trường hợp 1: Điểm M không thuộc d.
Vì đường trung trực d của đoạn thẳng MM’ đi qua điểm O nên O cách đều hai đầu mút hay OM = OM’.
Mà điểm M thuộc đường tròn (O; R) nên OM = R, do đó OM’ = R.
Vậy điểm M’ thuộc đường tròn (O; R).
Lời giải bài tập Toán 9 Bài 1: Đường tròn hay, chi tiết khác: