Giải Toán 9 trang 85 Tập 1 Chân trời sáng tạo
Với Giải Toán 9 trang 85 Tập 1 trong Bài 2: Tiếp tuyến của đường tròn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 85.
Giải Toán 9 trang 85 Tập 1 Chân trời sáng tạo
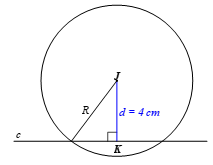
Thực hành 1 trang 85 Toán 9 Tập 1: Cho đường tròn (J; 5 cm) và đường thẳng c. Gọi K là chân đường vuông góc vẽ từ J xuống c, d là độ dài của đoạn thẳng JK. Xác định vị trí tương đối của đường thẳng c và đường tròn (J; 5 cm) trong mỗi trường hợp sau:
a) d = 4 cm;
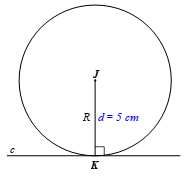
b) d = 5 cm;
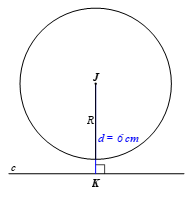
c) d = 6 cm.
Lời giải:
a)
Ta có d = 4 cm, R = 5 cm.
Vì d < R nên đường thẳng c cắt đường tròn (J; 5 cm) tại hai điểm.
b)
Ta có d = 5 cm, R = 5 cm.
Vì d = R nên đường thẳng c tiếp xúc với đường tròn (J; 5 cm) tại điểm K.
c)
Ta có d = 6 cm, R = 5 cm.
Vì d > R nên đường thẳng c và đường tròn (J; 5 cm) không giao nhau.
Vận dụng 1 trang 85 Toán 9 Tập 1: Một diễn viên xiếc đi xe đạp một bánh trên sợi dây cáp căng được cố định ở hai đầu dây. Biết đường kính bánh xe là 72 cm, tính khoảng cách từ trục bánh xe đến dây cáp.
Lời giải:
Do sợi dây tiếp xúc với bánh xe nên khoảng cách từ trục bánh xe đến dây cáp bằng bán kính bánh xe.
Vậy khoảng cách từ trục bánh xe đến dây cáp là:
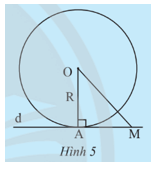
Khám phá 2 trang 85 Toán 9 Tập 1: Cho điểm A nằm trên đường tròn (O; R), đường thẳng d đi qua A và vuông góc với OA. Gọi M là một điểm trên d (M khác A).
a) Giải thích tại sao ta có OA = R và OM > R.
b) Giải thích tại sao d và (O) không thể có điểm chung nào khác ngoài A.
Lời giải:
a) Vì điểm A nằm trên đường tròn (O; R) nên OA = R.
Ta có OA vuông góc với đường thẳng d tại A nên OA là khoảng cách từ điểm O đến đường thẳng d.
Do OA, OM lần lượt là đường vuông góc, đường xiên kẻ từ O đến đường thẳng d nên OA < OM.
Mà OA = R nên OM > R.
b) Ta có OA = R nên d tiếp xúc với đường tròn (O; R) tại A.
Mà khi đường thẳng d tiếp xúc với đường tròn (O; R) thì đường thẳng d và đường tròn (O; R) có duy nhất một điểm chung.
Vậy d và (O) không thể có điểm chung nào khác ngoài A.
Lời giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác: