Giải Toán 9 trang 89 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 89 Tập 1 trong Bài 2: Tiếp tuyến của đường tròn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 89.

Giải Toán 9 trang 89 Tập 1 Chân trời sáng tạo

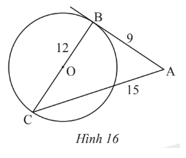
Bài 3 trang 89 Toán 9 Tập 1: Trong Hình 16, AB = 9, BC = 12, AC = 15 và BC là đường kính của đường tròn (O). Chứng minh AB là tiếp tuyến của đường tròn (O).

Lời giải:

Xét ∆ABC có:

⦁ AB² + BC² = 9² + 12² = 225;

⦁ AC² = 15² = 225.

Do đó AB² + BC² = AC²,

Theo định lí Pythagore đảo, ta có ∆ABC vuông tại B.

Suy ra AB ⊥ BC hay AB ⊥ OB.

Xét đường tròn (O) có AB ⊥ OB tại B thuộc đường tròn (O) nên AB là tiếp tuyến của đường tròn (O).

Bài 4 trang 89 Toán 9 Tập 1: Cho tam giác ABC có đường tròn (O) nằm trong và tiếp xúc với ba cạnh của tam giác. Biết AM = 6 cm, BP = 3 cm, CE = 8 cm (Hình 17). Tính chu vi tam giác ABC.

Lời giải:

Ta có:

⦁ AE, AM là hai tiếp tuyến của (O) cắt nhau tại A nên AE = AM = 6 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ BM, BP là hai tiếp tuyến của (O) cắt nhau tại B nên BM = BP = 3 cm (tính chất hai tiếp tuyến cắt nhau).

⦁ CP, CE là hai tiếp tuyến của (O) cắt nhau tại C nên CP = CE = 8 cm (tính chất hai tiếp tuyến cắt nhau).

Chu vi tam giác ABC là:

AB + BC + CA = AM + BM + BP + CP + CE + AE

= 6 + 3 + 3 + 8 + 8 + 6 = 34 (cm).

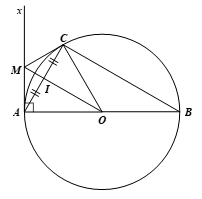
Bài 5 trang 89 Toán 9 Tập 1: Cho đường tròn (O; R) có đường kính AB. Vẽ dây AC sao cho AC = R. Gọi I là trung điểm của dây AC. Đường thẳng OI cắt tiếp tuyến Ax tại M. Chứng minh rằng:

a) $\widehat{\text{ACB}}$ có số đo bằng 90°, từ đó suy ra độ dài của BC theo R;

b) OM là tia phân giác của $\widehat{\text{COA}};$

c) MC là tiếp tuyến của đường tròn (O; R).

Lời giải:

a) Vì A, B, C cùng nằm trên đường tròn (O; R) có đường kính AB nên $OA=OB=OC=\frac{1}{2}AB=R$ và AB = 2R.

Xét ∆ABC có CO là đường trung tuyến ứng với cạnh AB và $OC=\frac{1}{2}AB$ nên ∆ABC là tam giác vuông tại C. Do đó $\widehat{ACB}=90°.$

Xét ∆ABC vuông tại C, theo định lí Pythagore, ta có: AB² = BC² + AC².

Suy ra BC² = AB² – AC² = (2R)² – R² = 3R².

Do đó $BC=\sqrt{3R^2}=R\sqrt{3}.$

b) Xét ∆OAC có OA = OC nên ∆OAC là tam giác cân tại O.

∆OAC cân tại O có OI là đường trung tuyến ứng với cạnh đáy nên đồng thời là đường phân giác của tam giác.

Do đó OM là tia phân giác của $\widehat{\text{COA}}.$

c) Xét ∆OAM và ∆OCM có:

OA = OC = R;

$\widehat{AOM}=\widehat{COM}$ (do OM là tia phân giác của $\widehat{\text{COA}});$

OM là cạnh chung.

Do đó ∆OAM = ∆OCM (c.g.c).

Suy ra $\widehat{OAM}=\widehat{OCM}$(hai góc tương ứng).

Mà $\widehat{OAM}=90°$ nên $\widehat{OCM}=90°.$

Do đó MC ⊥ OC tại C, lại có C thuộc (O; R) nên MC là tiếp tuyến của đường tròn (O; R).

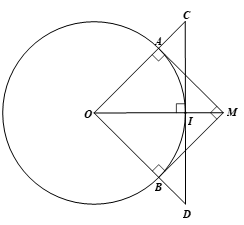
Bài 6 trang 89 Toán 9 Tập 1: Cho đường tròn (O; 5 cm) điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A, B là hai tiếp điểm) vuông góc với nhau tại M.

a) Tính độ dài của MA và MB.

b) Qua giao điểm I của đoạn thẳng MO và đường tròn (O), vẽ một tiếp tuyến cắt OA, OB lần lượt tại C, D. Tính độ dài của CD.

Lời giải:

Vì MA, MB lần lượt là hai tiếp tuyến của đường tròn (O) tại A, B nên MA ⊥ OA và MB ⊥ OB hay $\widehat{OAM}=90°;\widehat{OBM}=90°.$

Xét tứ giác OAMB có: $\widehat{OAM}=90°;\widehat{OBM}=90°;\widehat{AMB}=90°$(do MA ⊥ MB).

Do đó tứ giác OAMB là hình chữ nhật.

Lại có OA = OB = 5 cm (do A, B nằm trên đường tròn (O; 5 cm)).

Suy ra hình chữ nhật OAMB là hình vuông, nên MA = MB = OA = OB = 5 cm.

b) Vì OAMB là hình vuông nên $\widehat{AOB}=90°$ và OM là tia phân giác của góc AOB.

Do đó $\widehat{AOM}=\widehat{BOM}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}\cdot 90°=45°.$

Vì CD là tiếp tuyến của đường tròn (O) tại I nên CD ⊥ OI.

Xét ∆OCI vuông tại I, ta có: $CI=OI\cdot \tan \widehat{COI}=5\cdot \tan 45°=5\text{ (cm).}$

Xét ∆ODI vuông tại I, ta có: $DI=OI\cdot \tan \widehat{CDOI}=5\cdot \tan 45°=5\text{ (cm).}$

Vậy CD = CI + DI = 5 + 5 = 10 (cm).

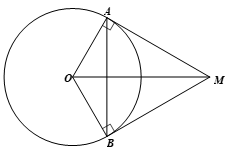
Bài 7 trang 89 Toán 9 Tập 1: Cho đường tròn (O), điểm M nằm ngoài (O) sao cho MA và MB là hai tiếp tuyến (A, B là hai tiếp điểm) thỏa mãn $\widehat{\text{AMB}}=60°.$ Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.

Lời giải:

Vì MA và MB là hai tiếp tuyến tại A, B của đường tròn (O) cắt nhau tại M nên MA = MB (tính chất hai tiếp tuyến cắt nhau).

Do đó ∆MAB cân tại M, lại có $\widehat{\text{AMB}}=60°$ nên ∆MAB là tam giác đều.

Suy ra MA = MB = AB.

Chu vi ∆MAB là: MA + MB + AB = 3AB.

Theo bài, chu vi tam giác MAB là 18 cm nên 3AB = 18, do đó AB = 6 (cm).

Vậy AB = 6 cm.

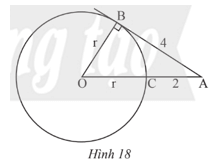
Bài 8 trang 89 Toán 9 Tập 1: Trong Hình 18, AB là tiếp tuyến của đường tròn (O) tại B.

a) Tính bán kính r của đường tròn (O).

b) Tính chiều dài cạnh OA của tam giác ABO.

Lời giải:

a) Vì AB là tiếp tuyến của đường tròn (O) tại B nên AB ⊥ OB tại B.

Xét ∆OAB vuông tại B, theo định lí Pythagore, ta có: OA² = OB² + AB²

Suy ra (OC + CA)² = OB² + AB²

Do đó (r + 2)² = r² + 4². (*)

Giải phương trình (*):

(r + 2)² = r² + 4²

r² + 4r + 4 = r² + 16

4r = 12

r = 3.

Vậy bán kính của đường tròn (O) là r = 3.

b) Ta có OA = OC + CA = r + 2 = 3 + 2 = 5 (cm).

Vậy OA = 5 cm.

Lời giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

• Giải Toán 9 trang 83
• Giải Toán 9 trang 85
• Giải Toán 9 trang 86
• Giải Toán 9 trang 87
• Giải Toán 9 trang 88