Giải Toán 9 trang 87 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 9 trang 87 Tập 1 trong Bài 2: Tiếp tuyến của đường tròn Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 87.

Giải Toán 9 trang 87 Tập 1 Chân trời sáng tạo

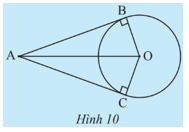
Khám phá 3 trang 87 Toán 9 Tập 1: Cho đường tròn (O) và hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau tại điểm A (Hình 10).

a) Chứng minh hai tam giác ABO và ACO bằng nhau.

b) Tìm các đoạn thẳng bằng nhau và các góc bằng nhau trong Hình 10.

Lời giải:

a) Vì AB, AC lần lượt là tiếp tuyến của đường tròn (O) tại B, C nên AB ⊥ OB và AC ⊥ OC.

Xét ∆ABO và ∆ACO có:

$\widehat{ABO}=\widehat{ACO}=90°;$

OB = OC (cùng là bán kính của đường tròn (O));

OA là cạnh chung.

Do đó ∆ABO = ∆ACO (cạnh huyền – cạnh góc vuông).

b) Theo câu a, ∆ABO = ∆ACO, suy ra:

⦁ OB = OC; AB = AC (hai cạnh tương ứng);

⦁ $\widehat{ABO}=\widehat{ACO}=90°; \widehat{BAO}=\widehat{CAO};\widehat{BOA}=\widehat{COA}$ (các cặp góc tương ứng).

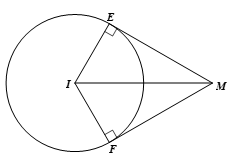
Thực hành 3 trang 87 Toán 9 Tập 1: Cho điểm M nằm ngoài đường tròn (I; 6 cm) và ME, MF là hai tiếp tuyến của đường tròn này tại E và F. Cho biết $\widehat{\text{EMF}}=60°.$

a) Tính số đo $\widehat{\text{EMI}}$ và $\widehat{\text{EIF}}.$

b) Tính độ dài MI.

Lời giải:

Vì ME, MF lần lượt là hai tiếp tuyến tại E, F của đường tròn (I) và cắt nhau tại M nên:

⦁ ME ⊥ IE tại E, MF ⊥ IF tại F hay $\widehat{IEM}=90°;\widehat{IFM}=90°;$

⦁ MI là tia phân giác của góc EMF. Do đó $\widehat{EMI}=\frac{1}{2}\widehat{EMF}=\frac{1}{2}\cdot 60°=30°.$

Xét tứ giác IEMF có: $\widehat{EIF}+\widehat{IEM}+\widehat{EMF}+\widehat{IFM}=360°$(tổng các góc của một tứ giác).

Suy ra $\widehat{EIF}=180°-\left(\widehat{IEM}+\widehat{EMF}+\widehat{IFM}\right)$

Hay $\widehat{EIF}=360°-\left(90°+60°+90°\right)=120°.$

b) Vì E thuộc đường tròn (I; 6 cm) nên IE = 6 cm.

Xét ∆IEM vuông tại E, ta có: $\sin \widehat{EMI}=\frac{IE}{MI}.$

Suy ra $MI=\frac{IE}{\sin \widehat{EMI}}=\frac{6}{\sin 30°}=12\text{ (cm).}$

Lời giải bài tập Toán 9 Bài 2: Tiếp tuyến của đường tròn hay khác:

• Giải Toán 9 trang 83
• Giải Toán 9 trang 85
• Giải Toán 9 trang 86
• Giải Toán 9 trang 88
• Giải Toán 9 trang 89