Vận dụng 3 trang 101 Toán 9 Tập 1 Chân trời sáng tạo

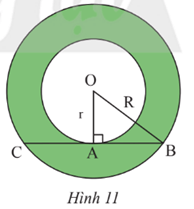
Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11).

Giải Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên - Chân trời sáng tạo

Vận dụng 3 trang 101 Toán 9 Tập 1: Cho hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) với R > r. Trên đường tròn (O; R) lấy hai điểm B, C sao cho BC vừa là dây cung của (O; R), vừa là tiếp tuyến của đường tròn (O; r) tại A (Hình 11).

a) Tính độ dài đoạn thẳng BC theo r và R.

b) Cho $BC=a\sqrt{3}.$ Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a.

Lời giải:

a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên BC ⊥ OA.

Xét ∆OBC có OB = OC nên ∆OBC cân tại O. Do đó đường cao OA đồng thời là đường trung tuyến của tam giác.

Suy ra A là trung điểm của BC nên BC = 2AB.

Xét ∆OAB vuông tại A, theo định lí Pythagore, ta có: OB² = OA² + AB².

Suy ra AB² = OB² – OA² = R² – r².

Do đó $AB=\sqrt{R^2-r^2}.$

Khi đó $BC=2\sqrt{R^2-r^2}.$

b) Theo bài, $BC=a\sqrt{3},$ do đó $2\sqrt{R^2-r^2}=a\sqrt{3}$

Suy ra $\sqrt{R^2-r^2}=\frac{a\sqrt{3}}{2}$ nên $R^2-r^2={\left(\frac{a\sqrt{3}}{2}\right)}^2=\frac{3a^2}{4}.$

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) là:

$S=\pi \left(R^2–r^2\right)=\pi \cdot \frac{3a^2}{4}=\frac{3\pi }{4}{a}^2.$

Lời giải bài tập Toán 9 Bài 4: Hình quạt tròn và hình vành khuyên hay, chi tiết khác:

• Khởi động trang 98 Toán 9 Tập 1: Số lượng cây ăn trái của trang trại Đất Lành được cho trong bảng sau: ....

• Khám phá 1 trang 98 Toán 9 Tập 1: Một hàng rào bao quanh một sân cỏ hình tròn có bán kính 10 m (Hình 1) được ghép bởi 360 phần bằng nhau ....

• Thực hành 1 trang 99 Toán 9 Tập 1: Tính độ dài cung 72° của một đường tròn có bán kính 25 cm ....

• Vận dụng 1 trang 99 Toán 9 Tập 1: Tính độ dài của đoạn hàng rào từ A đến B của sân cỏ trong Hình 3, cho biết $\widehat{AOB}=80°$ ....

• Khám phá 2 trang 99 Toán 9 Tập 1: a) Ta có thể tính diện tích của miếng bánh pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh hay không ....

• Thực hành 2 trang 100 Toán 9 Tập 1: Tính diện tích hình quạt tròn bán kính R = 20 cm, ứng với cung 72° ....

• Vận dụng 2 trang 100 Toán 9 Tập 1: Tính diện tích của miếng bánh pizza có dạng hình quạt tròn trong Hình 8. Biết OA = 15 cm ....

• Khám phá 3 trang 101 Toán 9 Tập 1: a) Vẽ đường tròn (C) tâm O bán kính r = 5 cm và đường tròn (C’) tâm O bán kính R = 8 cm ....

• Thực hành 3 trang 101 Toán 9 Tập 1: Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) (kết quả làm tròn ....

• Bài 1 trang 102 Toán 9 Tập 1: Tính độ dài các cung 30°; 90°; 120° của đường tròn (O; 6 cm) ....

• Bài 2 trang 102 Toán 9 Tập 1: Tính diện tích các hình quạt tròn ứng với cung có số đo lần lượt là 30°; 90°; 120° của hình tròn (O; 12 cm) ....

• Bài 3 trang 102 Toán 9 Tập 1: Tính diện tích các hình quạt tròn ứng với cung có độ dài lần lượt là 8 cm, 15 cm của hình tròn (O; 5 cm) ....

• Bài 4 trang 102 Toán 9 Tập 1: Tính diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 9 cm) và (O; 12 cm) ....

• Bài 5 trang 102 Toán 9 Tập 1: Tính diện tích hình viên phân giới hạn bởi dây cung có độ dài là 55 cm và cung có số đo là 95° ....

• Bài 6 trang 102 Toán 9 Tập 1: Một máy kéo nông nghiệp có đường kính bánh xe sau là 124 cm và đường kính bánh xe trước là 80 cm ....

• Bài 7 trang 102 Toán 9 Tập 1: Thành phố Đà Lạt nằm vào khoảng 11°58’ vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng ....