Tổng hợp lý thuyết Chương 2: Hàm số bậc nhất và bậc hai hay, chi tiết - Toán lớp 10

---

Tổng hợp lý thuyết Chương 2: Hàm số bậc nhất và bậc hai hay, chi tiết

Tài liệu Tổng hợp lý thuyết Chương 2: Hàm số bậc nhất và bậc hai hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Chương 2: Hàm số bậc nhất và bậc hai từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

• Lý thuyết Hàm số
• Lý thuyết Hàm số y = ax + b
• Lý thuyết Hàm số bậc hai
• Lý thuyết Tổng hợp Chương 2: Hàm số bậc nhất và bậc hai

Lý thuyết Hàm số

I. ÔN TẬP VỀ HÀM SỐ

1. Hàm số. Tập xác định của hàm số

Giả sử có hai đại lượng biếnthiên x và y, trong đó x nhận giá trị thuộc tập số D.

Nếu với mỗi giá trị của x thuộc tập D có một và chỉ một giá trị tương ứng của x thuộc tập số thực R thì ta có một hàm số.

Ta gọi x là biến số và y là hàm số của x.

Tập hợp D được gọi là tập xác định của hàm số.

2. Cách cho hàm số

Một hàm số có thể được cho bằng các cách sau.

Hàm số cho bằng bảng

Hàm số cho bằng biểu đồ

Hàm số cho bằng công thức

Tập xác định của hàm số y = f(x) là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

3. Đồ thị của hàm số

Đồ thị của hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x,f(x)) trên mặt phẳng tọa độ với x thuộc D.

II. SỰ BIẾN THIÊN CỦA HÀM SỐ

1. Ôn tập

Hàm số y = f(x) gọi là đồng biến (tăng) trên khoảng (a ; b) nếu

∀x₁, x₂ ∈ (a ; b) : x₁ < x₂ => f(x₁) < f(x₂)

Hàm số y = f(x) gọi là nghịch biến (giảm) trên khoảng (a ; b) nếu :

∀x₁, x₂ ∈ (a ; b) : x₁ < x₂ => f(x₁) > f(x₂)

2. Bảng biến thiên

Xét chiều biến thiên của một hàm số là tìm các khoảng đồng biến và các khoảng nghịch biến của nó. Kết quả xét chiều biến thiên được tổng kết trong một bảng gọi là bảng biến thiên.

Ví dụ. Dưới đây là bảng biến thiên của hàm số y = x².

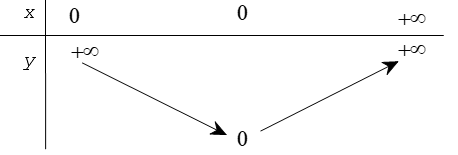
Hàm số y = x² xác định trên khoảng (hoặc trong khoảng) ( –∞ ; +∞) và khi x dần tới +∞ hoặc dần tới –∞ thì y đều dần tới +∞.

Tại x = 0 thì y = 0.

Để diễn tả hàm số nghịch biến trên khoảng (–∞ ; 0) ta vẽ mũi tên đi xuống (từ +∞ đến 0).

Để diễn tả hàm số đồng biến trên khoảng (0 ; +∞) ta vẽ mũi tên đi lên (từ 0 đến +∞).

Nhìn vào bảng biến thiên, ta sơ bộ hình dung được đồ thị hàm số (đi lên trong khoảng nào, đi xuống trong khoảng nào).

III. TÍNH CHẴN LẺ CỦA HÀM SỐ

1. Hàm số chẵn, hàm số lẻ

Hàm số y = f(x) với tập xác định D gọi là hàm số chẵn nếu

∀x ∈ D thì – x ∈ D và f( –x) = f(x)

Hàm số y = f(x) với tập xác định D gọi là hàm số lẻ nếu

∀x ∈ D thì – x ∈ D và f(–x) = – f(x)

2. Đồ thị của hàm số chẵn, hàm số lẻ

Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.

Đồ thị của một hàm số lẻ nhận gốc tọa độ là tâm đối xứng.

Lý thuyết Hàm số y = ax + b

I. ÔN TẬP VỀ HÀM SỐ BẬC NHẤT

y = ax + b (a ≠ 0)

Tập xác định D = R

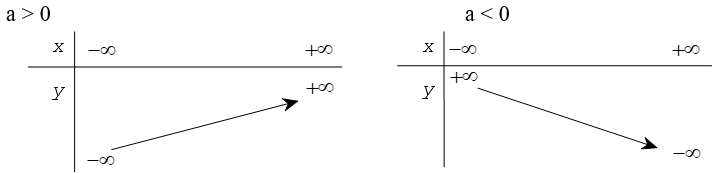
Chiều biến thiên

Với a > 0 hàm số đồng biến trên

Với a < 0 hàm số nghịch biến trên

Bảng biến thiên

Đồ thị

Đồ thị của hàm số là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng y = ax (nếu b ≠ 0) (nếu b ≠ 0) và đi qua hai điểm

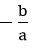
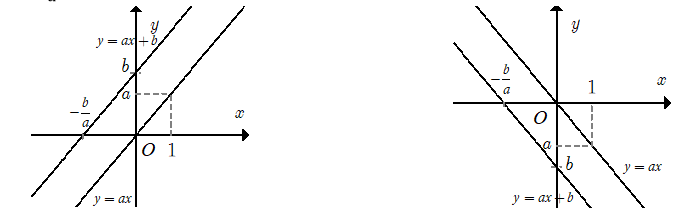
A(0 ; b), B( ; 0)

II. HÀM SỐ HẰNG y = b

Đồ thị hàm số y = b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm (0 ; b). Đường thẳng này gọi là đường thẳng y = b.

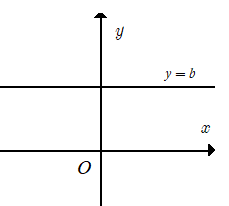
III. HÀM SỐ y = |x|

Hàm số y = |x| có liên quan chặt chẽ với hàm bậc nhất.

1. Tập xác định

Hàm số y = |x| xác định với mọi giá trị của x ∈ R tức là tập xác định y = |x|.

2. Chiều biến thiên

Theo định nghĩa của giá trị tuyệt đối, ta có y = |x| =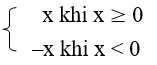

Từ đó suy ra hàm số y = |x| nghịch biến trên khoảng ( –∞ ; 0) và đồng biến trên khoảng (0 ; +∞).

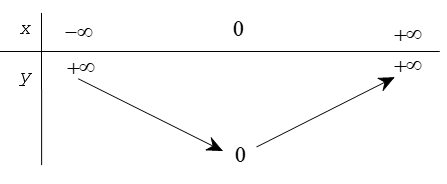
Bảng biến thiên

Khi x > 0 và dần tới +∞ thì y = x dần tới +∞, khi x < 0 dần tới –∞ thì y = –x cũng dần tới +∞. Ta có bảng biến thiên sau

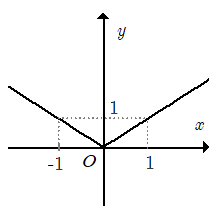
3. Đồ thị

Trong nửa khoảng [0; +∞) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = x.

Trong khoảng (–∞; 0) đồ thị của hàm số y = |x| trùng với đồ thị của hàm số y = –x

CHÚ Ý

Hàm số y = |x| là một hàm số chẵn, đồ thị của nó nhận Oy làm trục đối xứng.