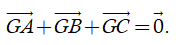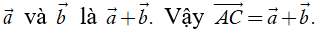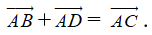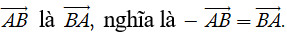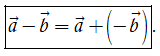Tổng hợp lý thuyết Chương 1: Vectơ hay, chi tiết - Toán lớp 10

---

Tổng hợp lý thuyết Chương 1: Vectơ hay, chi tiết

Tài liệu Tổng hợp lý thuyết Chương 1: Vectơ hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Chương 1: Vectơ từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

• Lý thuyết Các định nghĩa
• Lý thuyết Tổng và hiệu của hai vectơ
• Lý thuyết Tích của vectơ với một số
• Lý thuyết Hệ trục tọa độ
• Lý thuyết Tổng hợp Chương 1: Vectơ

Lý thuyết Các định nghĩa

1. Khái niệm vectơ

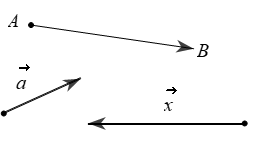
Cho đoạn thẳng AB. Nếu ta chọn điểm A làm điểu đầu, điểm B là điểm cuối thì đoạn thẳng AB có hướng từ A đến B. Khi đó ta nói AB là một đoạn thẳng có hướng.

Định nghĩa. Vectơ là một đoạn thẳng có hướng.

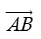
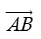
Vectơ có điểm đầu A, điểm cuối B được kí hiệu là và đọc là “ vectơ AB “. Để vẽ được vectơ ta vẽ đoạn thẳng AB và đánh dấu mũi tên ở đầu nút B.

Vectơ còn được kí hiệu là 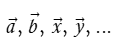khi không cần chỉ rõ điểm đầu và điểm cuối của nó.

2. Vectơ cùng phương, vectơ cùng hướng

Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

Định nghĩa. Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Nhận xét. Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi hai vectơ 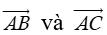cùng phương.

3. Hai vectơ bằng nhau

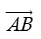
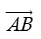
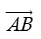
Mỗi vectơ có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vectơ đó. Độ dài của được kí hiệu là || , như vậy || = AB.

Vectơ có độ dài bằng 1 gọi là vectơ đơn vị.

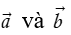
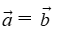
Hai vectơ được gọi là bằng nhau nếu chúng cùng hướng và có cùng độ dài, kí hiệu

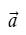
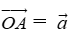
Chú ý. Khi cho trước vectơ và điểm O, thì ta luôn tìm được một điểm A duy nhất sao cho

4. Vectơ – không

Ta biết rằng mỗi vectơ có một điểm đầu và một điểm cuối và hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Bây giờ với một điểm A bất kì ta quy ước có một vectơ đặc biệt mà điểm đầu và điểm cuối đều là A. Vectơ này được kí hiệu là 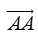và được gọi là vectơ – không.

Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ

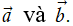
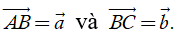
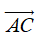
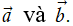
Định nghĩa. Cho hai vectơ Lấy một điểm A tùy ý, vẽ Vectơ được gọi là tổng của hai vectơ Ta kí hiệu tổng của hai vectơ

Phép toán tìm tổng của hai vectơ còn được gọi là phép cộng vectơ.

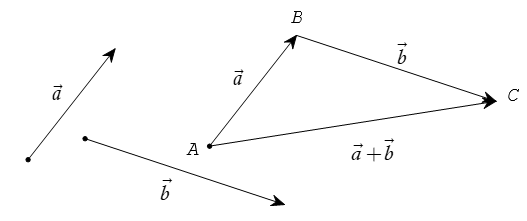
2. Quy tắc hình bình hành

Nếu ABCD là hình bình hành thì

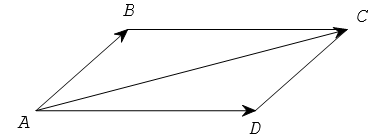
3. Tính chất của phép cộng các vectơ

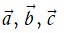
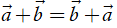
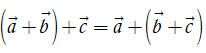
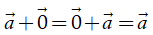
Với ba vectơ tùy ý ta có

• (tính chất giao hoán);

• (tính chất kết hợp);

• (tính chất của vectơ – không).

4. Hiệu của hai vectơ

a) Vectơ đối

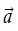
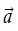
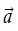
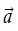
Cho vectơ Vectơ có cùng độ dài và ngược hướng với được gọi là vectơ đối của vectơ , kí hiệu là -.

Mỗi vectơ đều có vectơ đối, chẳng hạn vectơ đối của

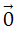
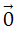
Đặc biệt, vectơ đối của vectơ là vectơ .

b) Định nghĩa hiệu của hai vectơ

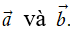
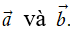
Định nghĩa. Cho hai vectơ Ta gọi hiệu của hai vectơ là vectơ

Như vậy

Từ định nghĩa hiệu của hai vectơ, suy ra với ba điểm O, A, B tùy ý ta có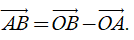

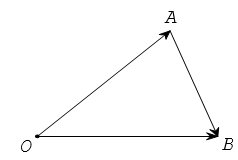
Chú ý:

1) Phép toán tìm hiệu của hai vectơ còn được gọi là phép trừ vectơ.

2) Với ba điểm tùy ý A, B, C ta luôn có

(quy tắc ba điểm);

(quy tắc trừ).

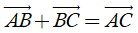
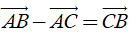
5. Áp dụng

a) Điểm I là trung điểm của đoạn thẳng AB khi và chỉ khi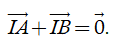

b) Điểm G là trọng tâm của tam giác ABC khi và chỉ khi