Tổng hợp lý thuyết Chương 3: Phương trình, Hệ phương trình hay, chi tiết - Toán lớp 10

---

Tổng hợp lý thuyết Chương 3: Phương trình, Hệ phương trình hay, chi tiết

Tài liệu Tổng hợp lý thuyết Chương 3: Phương trình, Hệ phương trình hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Chương 3: Phương trình, Hệ phương trình từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

• Lý thuyết Đại cương về phương trình
• Lý thuyết Phương trình quy về phương trình bậc nhất, bậc hai
• Lý thuyết Phương trình và hệ phương trình bậc nhất nhiều ẩn
• Lý thuyết Tổng hợp Chương 3: Phương trình, Hệ phương trình

Lý thuyết Đại cương về phương trình

I. KHÁI NIỆM PHƯƠNG TRÌNH

1. Phương trình một ẩn

Phương trình ẩn x là mệnh đề chứa biến có dạng

f(x) = g(x) (1)

trong đó f(x) và g(x) là những biểu thức của x. Ta gọi f(x) là vế trái, g(x) là vế phải của phương trình (1).

Nếu có số thực x0 sao cho f(x_o) = g(x_o) là mệnh đề đúng thì x_o được gọi là một nghiệm của phương trình (1).

Giải phương trình (1) là tìm tất cả các nghiệm của nó (nghĩa là tìm tập nghiệm).

Nếu phương trình không có nghiệm nào cả thì ta nói phương trình vô nghiệm (hoặc nói tập nghiệm của nó là rỗng).

2. Điều kiện của một phương trình

Khi giải phương trình (1), ta cần lưu ý với điều kiện đối với ẩn số x để f(x) và g(x) có nghĩa (tức là mọi phép toán đều thực hiện được). Ta cũng nói đó là điều kiện xác định của phương trình (hay gọi tắt là điều kiện của phương trình).

3. Phương trình nhiều ẩn

Ngoài các phương trình một ẩn, ta còn gặp những phương trình có nhiều ẩn số, chẳng hạn

3x + 2y = x² – 2xy + 8, (2)

4x² – xy + 2z = 3z² + 2xz + y² ( 3)

Phương trình (2) là phương trình hai ẩn (x và y), còn (3) là phương trình ba ẩn (x, y và z).

Khi x = 2, y = 1 thì hai vế của phương trình (2) có giá trị bằng nhau, ta nói cặp (x; y) = (2; 1) là một nghiệm của phương trình (2).

Tương tự, bộ ba số (x; y; z) = (–1; 1; 2) là một nghiệm của phương trình (3).

4. Phương trình chứa tham số

Trong một phương trình (một hoặc nhiều ẩn), ngoài các chữ đóng vai trò ẩn số còn có thể có các chữ khác được xem như những hằng số và được gọi là tham số.

II. PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG VÀ PHƯƠNG TRÌNH HỆ QUẢ

1. Phương trình tương đương

Hai phương trình được gọi là tương đương khi chúng có cùng tập nghiệm.

2. Phép biến đổi tương đương

Định lí

Nếu thực hiện các phép biển đổi sau đây trên một phương trình mà không làm thay đổi điều kiện của nó thì ta được một phương trình mới tương đương

a) Cộng hay trừ hai vế với cùng một số hoặc cùng một biểu thức;

b) Nhân hoặc chia hai vế với cùng một số khác 0 hoặc với cùng một biểu thức luôn có giá trị khác 0.

Chú ý: Chuyển vế và đổi dấu một biểu thức thực chất là thực hiện phép cộng hay trừ hai vế với biểu thức đó.

3. Phương trình hệ quả

Nếu mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình f₁(x) = g₁(x) thì phương trình f1(x) = g₁(x) được gọi là phương trình hệ quả của phương trình f(x) = g(x)

Ta viết

f(x) = g(x) => f₁(x) = g₁(x).

Phương trình hệ quả có thể có thêm nghiệm không phải là nghiệm của phương trình ban đầu. Ta gọi đó là nghiệm ngoại lai.

Lý thuyết Phương trình quy về phương trình bậc nhất, bậc hai

Bài giảng: Bài 2: Phương trình quy về phương trình bậc nhất, bậc hai - Thầy Lê Thành Đạt (Giáo viên VietJack)

I. ÔN TẬP VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI

1. Phương trình bậc nhất

Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau

Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn.

2. Phương trình bậc hai

Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau

3. Định lí Vi–ét

Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì

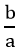
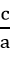
x₁ + x₂ = - , x₁x₂ = .

Ngược lại, nếu hai số u và v có tổng u + v = S và tích uv = P thì u và v là các nghiệm của phương trình

x² – Sx + P = 0.

II. PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI

Có nhiều phương trình khi giải có thể biến đổi về phương trình bậc nhất hoặc bậc hai.

Sau đây ta xét hai trong các dạng phương trình đó.

1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.

Ví dụ 1. Giải phương trình |x – 3| = 2x + 1. (3)

Giải

Cách 1

a) Nếu x ≥ 3 thì phương trình (3) trở thành x – 3 = 2x + 1. Từ đó x = –4.

Giá trị x = –4 không thỏa mãn điều kiện x ≥ 3 nên bị loại.

b) Nếu x < 3 thì phương trình (3) trở thành –x + 3 = 2x + 1. Từ đó x = .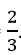

Giá trị này thỏa mãn điều kiện x < 3 nên là nghiệm.

Kết luận. Vậy nghiệm của phương trình là x =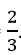

Cách 2. Bình phương hai vế của phương trình (3) ta đưa tới phương trình hệ quả

(3) => (x – 3)² = (2x + 1)²

=> x² – 6x + 9 = 4x² + 4x + 1

=> 3x² + 10x – 8 = 0.

Phương trình cuối có hai nghiệm là x = –4 và x =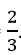

Thử lại ta thấy phương trình (3) chỉ có nghiệm là x =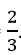

2. Phương trình chứa ẩn dưới dấu căn

Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.

Ví dụ 2. Giải phương trình 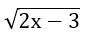= x – 2 (4).

Giải.

Điều kiện của phương trình (4) là x ≥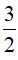

Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả

(4) => 2x – 3 = x² – 4x + 4

=> x² – 6x + 7 = 0.

Phương trình cuối có hai nghiệm là x = 3 + √2 và x = 3 – √2 . Cả hai giá trị này đều thỏa mãn điều kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x = 3 – √2 bị loại (vế trái dương còn vế phải âm), còn giá trị x= 3 + √2 là nghiệm (hai vế cùng bằng √2 + 1).

Kết luận. Vậy nghiệm của phương trình (4) là x= 3 + √2 .