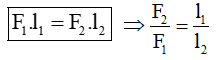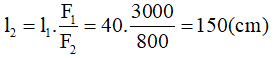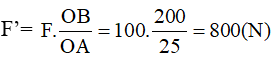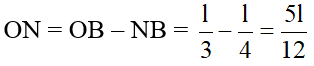Cách giải bài tập về Đòn bẩy cực hay
Cách giải bài tập về Đòn bẩy cực hay
Với Cách giải bài tập về Đòn bẩy cực hay Vật Lí lớp 8 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập từ đó đạt điểm cao trong bài thi môn Vật Lí 8.

A. Phương pháp giải
Học sinh cần nắm được các khái niệm về đòn bẩy, công thức đòn bẩy, công cơ học.
1. Công thức tính công cơ học
- Công cơ học phụ thuộc vào 2 yếu tố: Lực tác dụng vào vật và độ chuyển dời của vật.
- Công thức: A = F.s (khi vật chuyển dời theo hướng của lực)
Trong đó A: công của lực F
F: lực tác dụng vào vật (N)
s: quãng đường vật dịch chuyển (m)
- Đơn vị công là Jun (kí hiệu là J): 1J = 1 N.m.
2. Đòn bẩy.
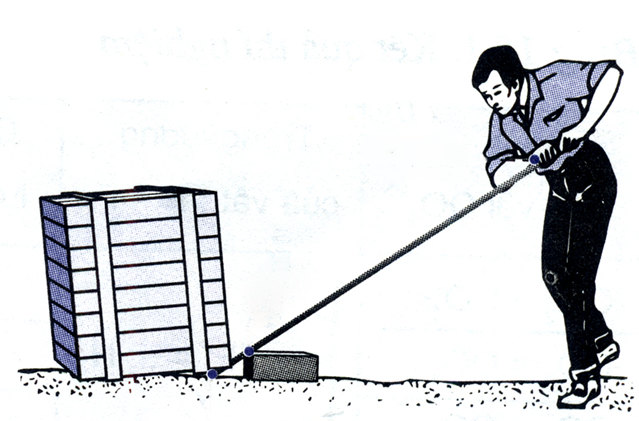
- Đòn bẩy là một loại máy cơ đơn giản. Đòn bẩy thông thường gồm một thanh dài và một điểm tựa.
- Người ta thường dùng đòn bẩy để nâng được các vật có trọng lượng lớn bằng lực nhỏ hơn trọng lượng vật.
- Dùng đòn bẩy được lợi bao nhiêu lần về lực thì thiệt bấy nhiêu lần về đường đi do đó không được lợi gì về công.
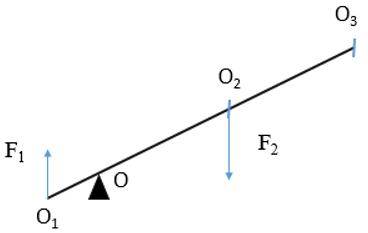
Trong đó F1; F2 là các lực tác dụng lên đòn bẩy, l1; l2 là các tay đòn của lực hay khoảng cách từ giá của các lực đến trục quay.
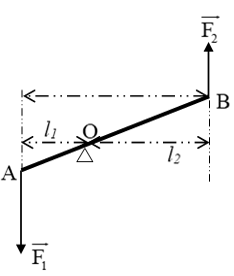
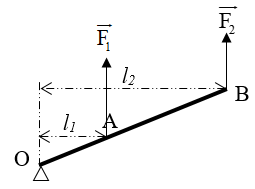
- Khoảng cách giữa điểm tựa O và phương của lực gọi là cánh tay đòn của lực
3. Phương pháp giải bài tập về đòn bẩy.
- Bước 1: Phân tích phương chiều các lực tác dụng vào cơ hệ trên hình vẽ.
- Bước 2: Chỉ rõ tên lực tác dụng, cường độ và đơn vị của mỗi lực, xác định được cánh tay đòn của lực, trục quay.
- Bước 3: Sử dụng phương trình cân bằng của đòn bẩy để giải bài tập.
B. Ví dụ minh họa
Ví dụ 1: Cái khuy vỏ chai nước ngọt thực chất là một:

A. mặt phẳng nghiêng
B. ròng rọc
C. đòn bẩy
D. palăng
Lời giải:
Đáp án C
Cái khuy nắp chai là một ứng dụng của đòn bẩy.
Ví dụ 2: Cân Rô béc van (cân đòn) là ứng dụng của máy cơ đơn giản nào?
A. Đòn bẩy
B. Mặt phẳng nghiêng
C. Ròng rọc
D. Cả ba đều không đúng
Lời giải:
Đáp án A

Cân Rô béc van (cân đòn) là ứng dụng của đòn bẩy với điểm tựa và các lực như trên hình vẽ.
Ví dụ 3: Người ta sử dụng một đòn bẩy như hình vẽ. Biết OO1 = 10cm; OO2 = 60cm. Người ta tác dụng vào điểm O2 lực có độ lớn 100N. Tính độ lớn lực F1 tại điểm O1 ?
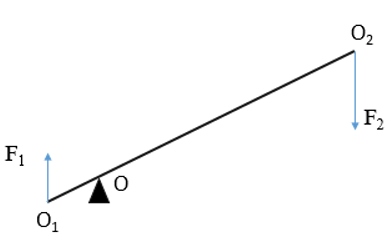
Lời giải:
- Áp dụng công thức đòn bẩy:
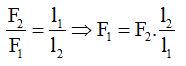
Độ lớn của lực F1 là:
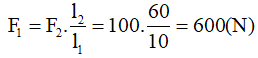
Câu 1: Một đòn bẩy như trên hình vẽ. Nếu tăng lực F2 lên 4 lần thì lực F1 sẽ thay đổi như thế nào?

A. Tăng lên 16 lần
B. Tăng lên 4 lần
C. Tăng lên 2 lần
D. Tăng lên mấy lần phụ thuộc vào tỷ lệ OO1 và OO2
Đáp án B
- Áp dụng công thức đòn bẩy:
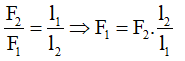
Nếu tăng lực F2 lên mấy lần thì lực F1 cũng sẽ tăng lên bấy nhiêu lần.
Câu 2: Một đòn bẩy như trên hình vẽ. Ban đầu lực F2 tác dụng vào điểm O2 thì ở O1 xuất hiện lực F1 có độ lớn 400N. Nếu dịch điểm đặt lực F2 vào điểm O3 (OO2 = O2O3) thì độ lớn lực F1 là:
A. 200N B. 100N
C. 800N D. 1600N
Đáp án C
- Ta có OO3 = 2.OO2
- Áp dụng công thức đòn bẩy:
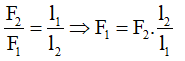
- Chiều dài cánh tay đòn tăng lên 2 lần thì lực F1 tăng lên 2 lần.
- Độ lớn lực F1 lúc này là: 400.2 = 800 (N)
Câu 3: Người ta dùng một đòn bẩy như hình vẽ để nâng một vật nặng. Biết OO2 = 4.OO1. Nếu tác dụng vào điểm O2 một lực có độ lớn 50N thì độ lớn lực F1 xuất hiện ở O1 là:
A. 50N B. 100N
C. 200N D. 400N
Đáp án C
- Áp dụng công thức đòn bẩy:
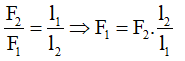
- Độ lớn lực F1 là:
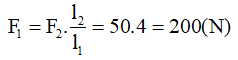
Câu 4: Để bẩy một hòn đá có khối lượng 1 tấn người ta sử dụng một đòn bẩy như trên hình vẽ. Biết OO2 = 5.OO1. Lực F2 tối thiểu tác dụng vào O2 là bao nhiêu để có thể nâng được tảng đá này lên?
A. 10000N B. 1000N
C. 200N D. 2000N
Đáp án D
1 tấn = 1000kg
- Trọng lượng của tảng đá là: 1000.10 = 10000 (N)
- Vậy để nâng được tảng đá này lên thì lực F1 tối thiểu phải là 10000N.
- Lực F2 tối thiểu phải là:
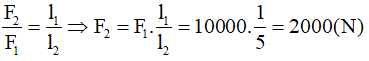
Câu 5: Một thanh nhẹ AB có thể quay tự do quanh một điểm O cố định với OA=2OB. Đầu A treo một vật có khối lượng 8 kg. Để hệ thống cân bằng người ta treo vào đầu B một vật có khổi lượng m (kg). Giá trị của m là:
A. 4kg B. 8kg
C. 16kg D. 32kg
Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
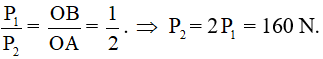
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)
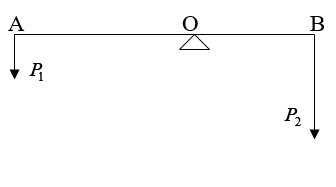
Câu 6: Muốn nâng một tảng đá có khối lượng 300kg, người ta phải dùng một đòn bẩy có chiều dài tối thiểu là bao nhiêu? Biết rằng điểm tựa O cách điểm đặt của tảng đá OA= 40cm và người thợ có sức đè tối ta là F = 800N.
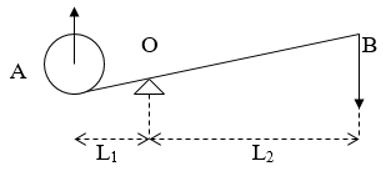
- Trọng lượng của tảng đá là: 300.10 = 3000 (N)
- Như vậy để nâng tảng đá lên được thì lực F1 tại điểm A nhỏ nhất là 3000N.
- Áp dụng công thức đòn bẩy:
- Lực tại điểm B lớn nhất là 800N
- Chiều dài l2 tối thiểu là:
- Chiều dài tối thiểu của đòn bẩy là: 40 + 150 = 190 (cm)
Đáp số: 190cm
Câu 7: Người ta dùng một xà beng có dạng như hình vẽ để nhổ một cây đinh cắm sâu vào gỗ. Biết OA = 25cm, OB = 200cm. Khi tác dụng một lực F = 100N vuông góc với OB tại đầu B ta sẽ nhổ được đinh. Tính lực giữ đinh của tấm gỗ?
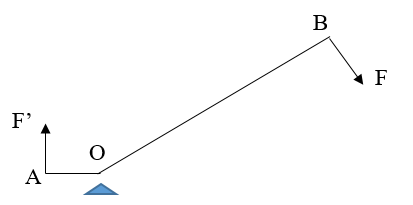
- Theo quy tắc cân bằng của đòn bẩy ta có:
F’.OA = F.OB
- Gọi Fc là lực cản của gỗ. Để nhổ được đinh thì lực F’ ≥ Fc. Khi F’ = 800N thì sẽ nhổ được đinh nên lực Fc = 800N
Đáp số: 800N
Câu 8: Một chiếc xà không đồng chất dài l = 16m, khối lượng 100 kg được tì hai đầu A, B lên hai bức tường. Trọng tâm của xà cách đầu A một khoảng GA = 4m. Hãy xác định lực đỡ của tường lên các đầu xà.
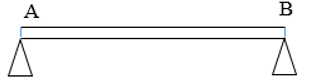
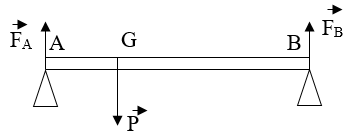
- Trọng lượng của xà bằng: P = 10.100 = 1000 (N)
- Trọng lượng của xà tập trung tại trọng tâm G của xà.
- Xà chịu tác dụng của 3 lực FA, FB, P
- Để xà đứng yên ta có:
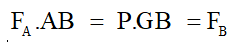
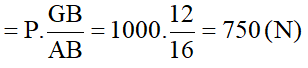
- Để tính FB ta coi xà là một đòn bẩy có điểm tựa tại A xà đứng yên khi:
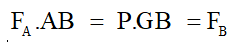
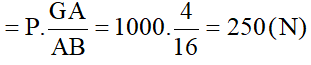
- Vậy lực đỡ của bức tường đầu A là 750 (N), của bức tường đầu B là 250 (N).
Đáp số: 750N và 250N
Câu 9: Một cái sào có khối lượng không đáng kể được treo theo phương nằm ngang bằng hai sợi dây AA’ và BB’. Tại điểm M người ta treo một vật nặng có khối lượng 70kg. Tính lực căng của các sợi dây AA’ và BB. Cho biết: AB = 1,4 m; AM = 0,2m.
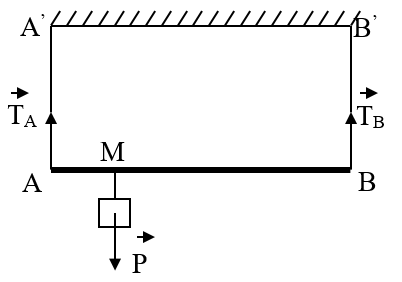
- Trọng lượng của vật nặng là: P = 10.70 = 700 (N)
- Gọi lực căng của các sợi dây AA’ và BB’ lần lượt là: TA và TB.
- Cái sào chịu tác dụng của 3 lực TA, TB và P.
- Để tính TA coi sào như một đòn bẩy có điểm tựa tại B.
- Để sào nằm ngang ta có:
TA.AB = P.MB
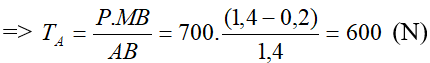
- Để tính TB coi A là điểm tựa. Để sào nằm ngang ta có:
TB.AB = P.MA
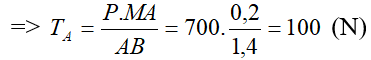
Vậy: Lực căng của sợi dây AA’ là 600 (N),sợi dây BB’ là 100 (N)
Đáp số: 600 (N); 100 (N)
Câu 10: Một thanh đồng chất, tiết diện đều, một đầu nhúng vào nước, đầu kia tựa vào thành chậu tại O sao cho OA = 1/2 OB. Khi thanh nằm cân bằng, mực nước ở chính giữa thanh. Tìm khối lượng riêng D của thanh, biết khối lượng riêng của nước là D0 = 1000kg/m3.
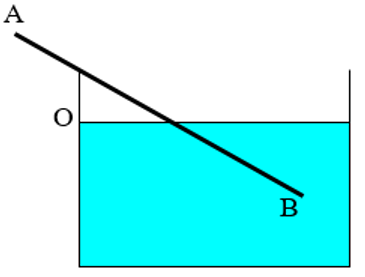
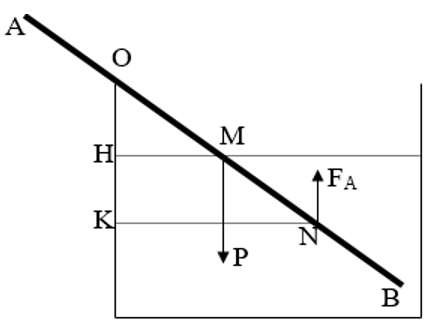
- Thanh chịu tác dụng của trọng lực P đặt tại trung điểm M của thanh AB và lực đẩy Acsimet đặt tại trung điểm N của MB. Thanh có thể quay quanh O. áp dụng quy tắc cân bằng của đòn bẩy ta có:
P. MH = F. NK (1).
- Gọi S là tiết diện và l là chiều dài của thanh ta có:
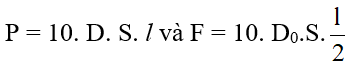
- Thay vào (1) ta có:
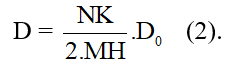
- Mặt khác:
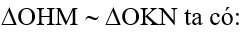
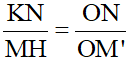
- Trong đó:
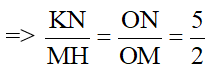
- thay vào (2) ta được:
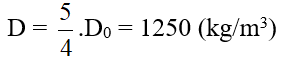
Đáp số: 1250 kg/m3