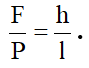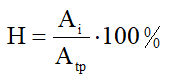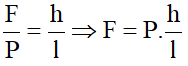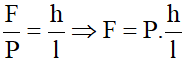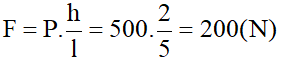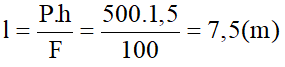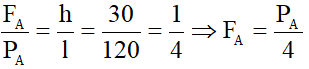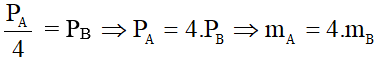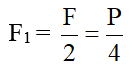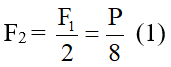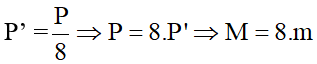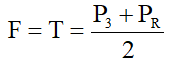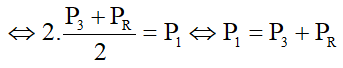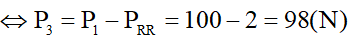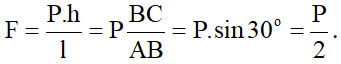Cách giải bài tập về Mặt phẳng nghiêng cực hay
Cách giải bài tập về Mặt phẳng nghiêng cực hay
Với Cách giải bài tập về Mặt phẳng nghiêng cực hay Vật Lí lớp 8 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập từ đó đạt điểm cao trong bài thi môn Vật Lí 8.

A. Phương pháp giải
Học sinh cần nắm được các tác dụng của ròng rọc, công cơ học.
1. Công thức tính công cơ học
- Công cơ học phụ thuộc vào 2 yếu tố: Lực tác dụng vào vật và độ chuyển dời của vật.
- Công thức: A = F.s ( khi vật chuyển dời theo hướng của lực)
- Trong đó A: công của lực F
F: lực tác dụng vào vật (N)
s: quãng đường vật dịch chuyển (m)
- Đơn vị công là Jun (kí hiệu là J): 1J = 1 N.m.
2. Mặt phẳng nghiêng:



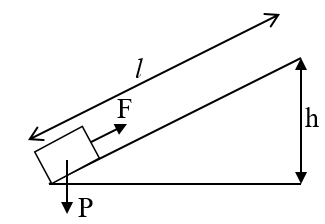
- Nếu ma sát không đáng kể, dùng mặt phẳng nghiêng được lợi bao nhiêu lần về lực thì thiệt bấy nhiêu lần về đường đi, không được lợi gì về công.
- Hiệu suất của mặt phẳng nghiêng:
Ví dụ 1: Khi sử dụng mặt phẳng nghiêng để kéo vật, muốn kéo vật lên cao với lực nhỏ hơn thì ta phải:
A. tăng độ cao mặt phẳng nghiêng
B. giữ nguyên độ dài mặt phẳng nghiêng
C. dùng nhiều người cùng kéo vật
D. giảm độ nghiêng của mặt phẳng nghiêng
Lời giải:
Đáp án D
- Vì:
- Độ nghiêng của mặt phẳng nghiêng càng giảm thì tỷ số 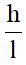
Ví dụ 2: Cách nào sau đây không làm giảm độ nghiêng mặt phẳng nghiêng?
A. Giảm chiều dài, giữ nguyên độ cao của mặt phẳng nghiêng.
B. Tăng chiều dài, giảm độ cao của mặt phẳng nghiêng.
C. Giảm chiều cao, giữ nguyên độ dài của mặt phẳng nghiêng
D. Vừa giảm độ cao, vừa tăng chiều dài của mặt phẳng nghiêng.
Lời giải:
Đáp án A
- Nếu giảm chiều dài, giữ nguyên độ cao của mặt phẳng nghiêng thì độ nghiêng của mặt phẳng nghiêng tăng chứ không giảm.
Ví dụ 3: Để đưa một thùng hàng lên xe tải, một người đã dùng lần lượt 4 tấm ván làm mặt phẳng nghiêng. Biết với 4 tấm ván người đó đã đẩy thùng hàng lên xe với 4 lực khác nhau: F1=1000N; F2 = 200N; F3 = 500N; F4 = 1200N. Bỏ qua ma sát giữa thùng hàng và tấm ván. Kết luận nào dưới đây là chính xác?

A. Tấm ván thứ nhất dài nhất
B. Tấm ván thứ hai dài nhất
C. Tấm ván thứ ba dài nhất
D. Tấm ván thứ tư dài nhất
Lời giải:
Đáp án B
Vì đưa thùng hàng lên cùng độ cao, mà tấm ván thứ hai cần lực kéo nhỏ nhất nên suy ra độ nghiêng của tấm thứ hai nhỏ nhất. Từ đó suy ra chiều dài của tấm ván thứ hai là lớn nhất
C. Bài tập vận dụng
Câu 1: Trong các trường hợp sau, trường hợp nào không phải là ứng dụng của mặt phẳng nghiêng?
A. Cầu trượt trong công viên nước
B. Cầu thang xoắn.
C. Cái mở nắp chai
D. Đường ngoằn nghèo bên sườn núi
Đáp án C
Cầu trượt, cầu thang xoắn, đường bên sườn núi là các ứng dụng của mặt phẳng nghiêng
Câu 2: Sử dụng mặt phẳng nghiêng để đưa 1 vật lên cao thiệt hại gì?
A. Đường đi
B. Lực
C. Trọng lực
D. Khối lượng
Đáp án A
Dùng mặt phẳng nghiêng cho ta lợi về lực nhưng bị thiệt hại về đường đi.
Câu 3: Người ta dùng một mặt phẳng nghiêng cao 2m, dài 5m để kéo một thùng hàng nặng 50kg lên cao. Bỏ qua ma sát. Lực cần thiết để kéo thùng hàng là:

A. 500N B. 1250N
C. 250N D. 200N
Đáp án D
- Trọng lượng thùng hàng là:
50.10 = 500 (N)
- Áp dụng công thức:
- Lực cần thiết để kéo thùng hàng là:
Câu 4: Để kéo một thùng dầu có khối lượng 50kg lên độ cao 1,5m người ta dùng một tấm gỗ phẳng làm mặt phẳng nghiêng. Biết lực dùng để kéo thùng dầu có độ lớn là 100N. Bỏ qua ma sát giữa tấm gỗ và thùng hàng. Chiều dài của tấm gỗ là:
A. 1,5m B. 5m
C. 7,5m D. 10m
Đáp án C
- Trọng lượng thùng hàng là:
50.10 = 500 (N)
- Áp dụng công thức:
- Chiều dài tấm gỗ là:
Câu 5: Hai vật A, B có cùng khối lượng nằm trên hai mặt phẳng nghiêng và được nối với nhau bằng một sợi dây vắt qua một ròng rọc (hình vẽ). Chiều dài mặt phẳng nghiêng có vật A là lA; chiều dài mặt phẳng nghiêng có vật B là lB. Kết luận nào dưới đây là đúng?
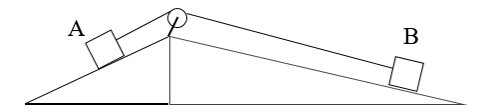
A. Vật B di chuyển xuống dưới vì lB > lA
B. Vật B di chuyển lên trên vì vật B ở phía dưới vật A
C. Vật A di chuyển xuống dưới vì lB > lA
D. Vật A di chuyển lên trên vì vật A ở phía trên vật B
Đáp án C
- Vì lB > lA nên lực để kéo vật B đi lên sẽ nhỏ hơn lực kéo vật A đi lên. Do đó vật B sẽ đi lên còn vật A sẽ đi xuống dưới.
Câu 6: Tại sao những con đường dốc lên đỉnh núi người ta không làm thẳng từ chân núi lên đỉnh núi mà phải làm theo hình zích zắc (như trong hình):

- Vì các con đường dốc lên núi chính là một mặt phẳng nghiêng. Khi độ nghiêng của mặt phẳng nghiêng càng nhỏ (chiều dài mặt phẳng nghiêng lớn) thì lực cần thiết để đưa vật lên cao càng nhỏ.
- Do đó người ta làm các con đường này ngoằn nghèo để tăng chiều dài con đường, dẫn đến lực cần thiết để các phương tiện di chuyển trên đường sẽ nhỏ hơn so với làm thẳng từ chân lên đỉnh núi
Câu 7: Một hệ ròng rọc, mặt phẳng nghiêng như trên hình vẽ. Hai vật A và B ở hình vẽ đứng yên. Cho biết MN = 120cm, NH = 30cm. Tính tỉ số khối lượng của hai vật B và A? Biết rằng ma sát và khối lượng dây là không đáng kể.
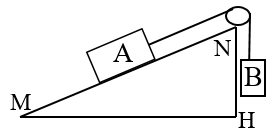
- Lực do vật kéo dây xuống dọc theo mặt phẳng nghiêng là :
- Lực do vật B kéo dây xuống là FB = PB
- Hai lực kéo này phải bằng nhau nên ta có:
- Ta suy ra tỉ số khối lượng của hai vật là:
mA : mB = 4
Đáp số: mA : mB = 4
Câu 8: Cho hệ thống như hình vẽ. Góc nghiêng α = 30°, dây và ròng rọc là lý tưởng, ỏ qua mọi ma sát. Cho khối lượng m = 5kg. Xác định khối lượng của vật M để hệ thống cân bằng?
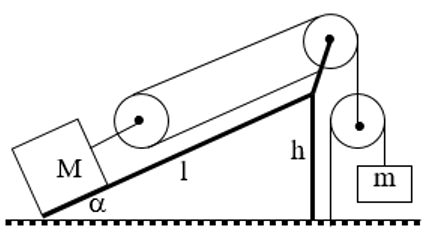
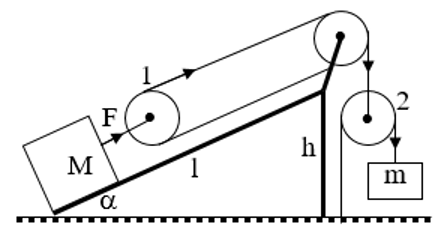
- Gọi P, P’ là trọng lượng của vật M và vật m
- Muốn hệ thống cân bằng thì: F = P.(h/l)
- Ta lại có h/l = sinα = sin30° = 1/2
⇒ F = P/2
- Lực kéo của mỗi dây vắt qua ròng rọc 1 là:
- Lực kéo của mỗi dây vắt qua ròng rọc 2 là:
- Lực kéo do chính trọng lượng P’ của m gây ra, tức là : P’ = F2 (2)
- Từ (1) và (2) suy ra:
Khối lượng của vật M là:
8. 5 = 40 (kg)
Đáp số: 40kg
Câu 9: Cho hệ thống như hình vẽ. Biết khối lượng của mỗi ròng rọc, vật m1 và vật m2 lần lượt là 0,2 kg; 10kg và 8kg, AB = 2.BC, bỏ qua ma sát và khối lượng của các dây nối. Hỏi hệ thống có cân bằng không ? Tại sao?
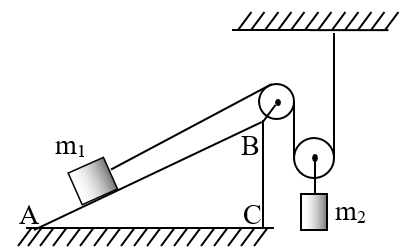
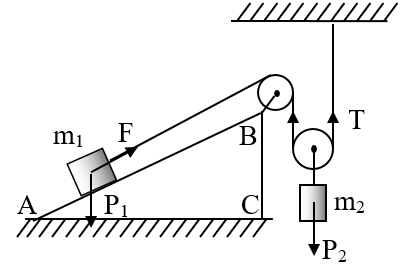
- Giả sử khi thay m2 bằng m3 sao cho hệ thống cân bằng.
- Gọi P1; P3; PR là trọng lượng của vật m1; m3 và ròng rọc
- Khi hệ thống cân bằng thì:
F.AB = P1.BC
⇔ F.2.BC = P1.BC ⇒ 2.F = P1
Mà ta có:
⇒ m3 = 9,8(kg)
- Vậy để hệ cân bằng thì cần phải treo vào ròng rọc 2 một vật có khối lượng 9,8kg.
- Do m2 = 8kg < 9,8kg nên khi treo m2 vào ròng rọc thì hệ thống không cân bằng mà vật m1 sẽ chuyển động xuống dưới còn m2 sẽ chuyển động lên trên.
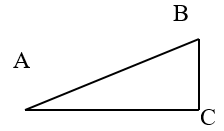
Câu 10: Một vật hình trụ có thể lăn không ma sát trên một mặt phẳng nghiêng AB như hình vẽ. Người ta nhận thấy khi góc nghiêng α = 0° thì lò xo dài l0 = 40cm và khi α = 90° thì lò xo dài 50cm. Biết độ dãn của lò xo tỉ lệ thuận với lực tác dụng vào đầu lò xo. Nếu α = 30° thì chiều dài của lò xo là bao nhiêu?
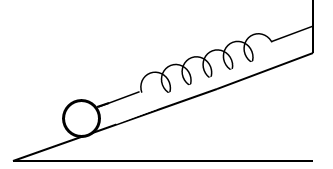
- Chiều dài l0 = 20 cm (khi α = 0°) chính là chiều dài tự nhiên của lò xo, tức là chiều dài của lò xo khi chưa bị tác dụng lực.
- Chiều dài l = 26cm (khi α = 90°)chính là chiều dài của lò xo khi nó bị tác dụng một lực bằng trọng lượng P của vật.
- Suy ra trọng lượng P đã làm lò xo dãn ra:
50 – 40 = 10 (cm)
- Coi mặt phẳng nghiêng là tam giác ABC với góc A = 30° thì lực kéo lò xo là lực F được tính như sau :
Nếu lực P làm lò xo dãn 10cm thì lực F = P/2 làm lò xo dãn thêm x cm.
- Do độ dãn của lò xo tỉ lệ thuận với lực tác dụng vào đầu lò xo ⇒ x = 5cm .
- Vậy chiều dài của lò xo khi α = 30° là:
l1 = 40 + 5 = 45 (cm)
Đáp số: 45cm