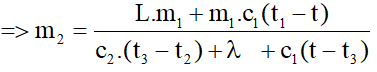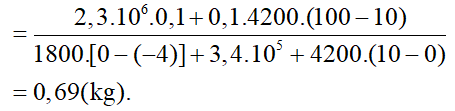Tìm nhiệt độ cân bằng của hỗn hợp trong bài toán chuyển thể

---

Tìm nhiệt độ cân bằng của hỗn hợp trong bài toán chuyển thể

Với Tìm nhiệt độ cân bằng của hỗn hợp trong bài toán chuyển thể Vật Lí lớp 8 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập từ đó đạt điểm cao trong bài thi môn Vật Lí 8.

A. Phương pháp giải

Học sinh cần nắm được kiến thức về nhiệt năng, nhiệt lượng, nguyên lý truyền nhiệt và phương trình cân bằng nhiệt

1. Nguyên lý truyền nhiệt

Khi hai vật có trao đổi nhiệt với nhau thì:

- Nhiệt truyền từ vật có nhiệt độ cao hơn sang vật có nhiệt độ thấp hơn.

- Sự truyền nhiệt xảy ra cho tới khi nhiệt độ của hai vật bằng nhau thì ngừng lại.

- Nhiệt lượng do vật này tỏa ra bằng nhiệt lượng do vật kia thu vào.

2. Phương trình cân bằng nhiệt

Q_{tỏa ra} = Q_{thu vào} Hay: C₁λ.m₁(t₁-t)=C₂λ.m₂(t-t₂)

Q_{tỏa ra} : tổng nhiệt lượng của các vật tỏa ra.

Q_{thu vào}: tổng nhiệt lượng của các vật thu vào.

   t: nhiệt độ khi cân bằng nhiệt

   t₁: nhiệt độ của vật tỏa nhiệt

   t₂: nhiệt độ của vật thu nhiệt

   C₁; C₂: nhiệt dung riêng của các chất

3. Sự chuyển thể của các chất

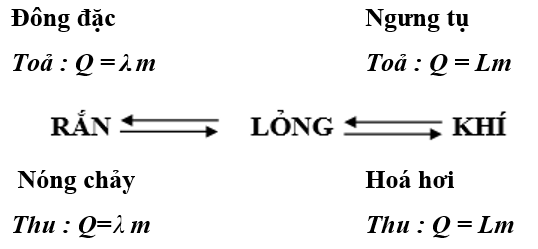
Q = λm : nhiệt lượng của vật thu vào hay toả ra ở nhiệt độ nóng chảy. (J)

Q = Lm : nhiệt lượng của vật thu vào hay toả ra ở nhiệt độ sôi.(J)

   λ: nhiệt nóng chảy của chất cấu tạo nên vật(J/kg)

   L : nhiệt hoá hơi của chất cấu tạo nên vật (J/kg)

- Khi chuyển từ thể rắn sang thể lỏng và ngược lại thì thể tích của vật có thể thay đổi nhưng khối lượng của vật luôn không thay đổi.

- Trong suốt quá trình chuyển thể thì nhiệt độ của vật luôn không thay đổi và đồ thị biểu diễn sự phụ thuộc của nhiệt độ vào nhiệt lượng cung cấp cho vật là một đường thẳng nằm ngang.

B. Ví dụ minh họa

Ví dụ 1: Người ta cho vào nhiệt lượng kế một hỗn hợp m₁ = 2 kg nước ở nhiệt độ t₁ = 25°C và m₂ = 1kg nước đá ở nhiệt độ t₂ = -20°C. Bỏ qua sự tỏa nhiệt ra môi trường xung quanh và nhiệt dung của nhiệt lượng kế. Xác định nhiệt độ cân bằng t của hỗn hợp khi đó? Biết nhiệt dung riêng của nước, của nước đá và nhiệt nóng chảy của nước đá lần lượt là C₁ = 4,2 kJ/kg.K; C₂ = 2,1 kJ/kg.K và λ = 340 kJ/Kg.

Lời giải:

- Nhiệt lượng toả ra của m₁ kg nước để hạ nhiệt độ tới 0°C là :

   Q₁ = C₁m₁(t₁ - 0) = 4,2.2 (25 - 0) = 210 (kJ).

- Nhiệt lượng cần cung cấp để 1kg nước đá tăng nhiệt độ tới 0°C là:

   Q₂ = C₂m₂(0 - t₂) = 2,1.1. [ 0 – (-20)] = 42(kJ)

- So sánh Q_thu và Qtoả ta thấy Q₁ > Q₂. Vậy nước đá bị nóng chảy.

- Nhiệt lượng cần để nước đá nóng chảy hoàn toàn là :

   Q₃ = λ.m₂ = 340.1 = 340 (kJ)

- So sánh ta thấy Q₁ < Q₂ + Q₃ . Vậy nước đá chưa nóng chảy hoàn toàn.

- Vậy nhiệt độ cân bằng là 0°C.

Đáp số: 0°C.

Ví dụ 2: Thả một khối nước đá có khối lượng m₂ = 0,2kg có nhiệt độ t₂ = -20°C vào m₁ = 2 kg nước ở nhiệt độ t₁ = 25°C. Bỏ qua sự tỏa nhiệt ra môi trường xung quanh Xác định nhiệt độ cân bằng t của hỗn hợp khi đó. Biết nhiệt dung riêng của nước, của nước đá và nhiệt nóng chảy của nước đá lần lượt là C₁ = 4,2 kJ/kg.K; C₂ = 2,1 kJ/kg.K và λ = 340 kJ/Kg.

Lời giải:

-Nhiệt lượng toả ra của 2kg nước để hạ nhiệt độ tới 0°C là:

   Q₁= m₁C₁(t₁ - 0) = 4,2.2(25 - 0)= 210 (kJ)

- Nhiệt lượng cần cung cấp để 0,2kg nước đá tăng nhiệt độ tới 0°C là:

   Q₂= m₂C₂(0 – t₂)= 2,1.0,2.[0 - (-20)]= 8,4 (kJ)

- So sánh: Q₁ > Q₂ : vậy nước đá phải nóng chảy.

- Nhiệt lượng cần cung cấp cho nước đá nóng chảy hoàn toàn là:

   Q₃ = λ.m₂ = 340.0,2 = 68(kJ)

-So sánh Q₁ > Q₂ + Q₃ : Điều này chứng tỏ toàn bộ khối lượng nước đá m₂ nóng lên đến 0°C, tan ra hoàn toàn rồi nóng lên đến t °C nào đó.

- Ta có phương trình cân bằng nhiệt:

   m₁C₁(t₁ – t) = m₂C₂(0 - t₂) + λ.m₂ + m₂C₁(t - 0)

⇒ m₁C₁(t₁ – t) = 8,4 + 68 + m₂C₁(t - 0) = 76,4 + m₂C₁(t - 0)

⇒ m₁C₁t₁ - 76,4 = C₁t.(m₁ + m₂)

⇒ 210 - 76,4 = 4,2.t.2,2

⇒ t = 14,46 (°C)

Đáp số: t = 14,46 (°C)

Ví dụ 3: Người ta cho vào nhiệt lượng kế một hỗn hợp m₁ = 2 kg nước ở nhiệt độ t₁ = 25°C và m₂ = 6kg nước đá ở nhiệt độ t₂ = -20°C. Bỏ qua sự tỏa nhiệt ra môi trường xung quanh và nhiệt dung của nhiệt lượng kế. Xác định nhiệt độ cân bằng t của hỗn hợp khi đó? Biết nhiệt dung riêng của nước, của nước đá và nhiệt nóng chảy của nước đá lần lượt là C₁ = 4,2 kJ/kg.K; C₂ = 2,1 kJ/kg.K và λ = 340 kJ/Kg.

Lời giải:

- Nhiệt lượng toả ra của 2kg nước để hạ nhiệt độ tới 0°C là:

   Q₁= m₁C₁(t₁ - 0) = 4,2.2(25 - 0)= 210 (kJ)

- Nhiệt lượng thu vào của nước đá để tăng nhiệt độ lên 0°C là:

   Q₂= m₂C₂(0 – t₂) = 2,1.6.[0 - (-20)]= 252(kJ)

- So sánh Q₁ < Q₂ : Điều này chứng tỏ nước hạ nhiệt độ tới 0°C sau đó đông đặc.

- Nhiệt lượng tỏa ra khi 2kg nước đông đặc là:

   Q₃ = λ.m = 340.2 = 680 (kJ)

- So sánh Q₁ + Q₃ > Q₂. Điều này chứng tỏ nước chưa đông đặc hoàn toàn.

- Vậy nhiệt độ của hỗn hợp sau khi cân bằng là 0°C.

Đáp số: 0°C.

C. Bài tập vận dụng

Câu 1: Cho một chậu nhỏ bằng thuỷ tinh khối lượng m = 100g có chứa m₁ = 500g nước ở nhiệt độ t₁ = 20°C và một cốc dùng để chứa những viên nước đá có cùng khối lượng m₂ = 20g ở nhiệt độ t₂ = - 5°C. Thả hai viên nước đá vào chậu. Cho nhiệt dung riêng của thủy tinh, nước và nước đá lần lượt là C = 2500 J/kg.K, C₁ = 4200J/kg.K và C₂ = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.10⁵J/kg (bỏ qua sự trao đổi nhiệt với cốc và môi trường bên ngoài). Kết luận nào sau đây là chính xác nhất?

A. Có một phần nước bị đông đặc thành nước đá

B. Hai viên đá tan hoàn toàn, nhiệt độ hỗn hợp là 0°C

C. Hai viên đá chưa tan hoàn toàn, nhiệt độ hỗn hợp là 0°C

D. Hai viên đá tan hoàn toàn, nhiệt độ hỗn hợp lớn hơn 0°C

Hiển thị đáp án

Đáp án: D

- Khi thả hai viên nước đá vào chậu nước. Giả sử nước đá tan hết ở 0°C.

- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0°C là:

   Q₁ = (mc + m₁c₁ )(t₁ – 0) = 47000 (J)

- Nhiệt lượng thu vào của 2 viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:

   Q₂= 2m₂C₂(0 – t₂) + 2m₂.λ = 13960 (J)

- Vì Q₁ > Q₂ nên 2 viên đá sẽ tan hết và nhiệt độ cân bằng 0°C < t < 20°C.

Câu 2: Cho một chậu nhỏ bằng thuỷ tinh khối lượng m = 150g có chứa m₁ = 750g nước ở nhiệt độ t₁ = 20°C. Người ta thả vào chậu một khối nước đá có khối lượng m₂ = 300g ở nhiệt độ t₂ = - 5°C. Cho nhiệt dung riêng của thủy tinh, nước và nước đá lần lượt là C = 2500 J/kg.K, C₁ = 4200J/kg.K và C₂ = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.10⁵J/kg (bỏ qua sự trao đổi nhiệt với cốc và môi trường bên ngoài). Kết luận nào sau đây là chính xác nhất?

A. Khối nước đá chưa tan hết

B. Khối nước đá đã tan hết, nhiệt độ hỗn hợp lớn hơn 0°C

C. Khối nước đá đã tan hết, nhiệt độ hỗn hợp đúng bằng 0°C

D. Không đủ cơ sở để kết luận

Hiển thị đáp án

Đáp án: A

- Nhiệt lượng do chậu và nước toả ra để hạ nhiệt độ xuống 0°C là:

   Q₁ = (mc + m₁c₁ )(t₁ – 0) = 70500 (J)

- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:

   Q₂= m₂C₂(0 – t₂) + m₂.λ = 104700 (J)

- Vì Q₂ > Q₁ nên khối nước đá chưa tan hết

Câu 3: Một chiếc xô bằng nhựa khối lượng m = 500g có chứa m₁ = 5kg nước ở nhiệt độ t₁ = 30°C và những viên nước đá có cùng khối lượng m₂ = 200g ở nhiệt độ t₂ = - 6°C. Cho nhiệt dung riêng của nhựa, nước và nước đá lần lượt là C = 5000 J/kg.K, C₁ = 4200J/kg.K và C₂ = 1800J/kg.K. Nhiệt nóng chảy của nước đá là λ = 3,4.10⁵J/kg (bỏ qua sự trao đổi nhiệt với môi trường bên ngoài). Người ta thả những viên đá vào trong xô. Hỏi phải thả vào xô ít nhất bao nhiêu viên nước đá để nhiệt độ cuối cùng trong xô là 0°C?

A. 8 viên      B. 9 viên

C. 10 viên      D. 11 viên

Hiển thị đáp án

Đáp án: B

- Nhiệt lượng do xô và nước toả ra để hạ nhiệt độ xuống 0°C là:

   Q₁ = (mc + m₁c₁ )(t₁ – 0) = 705000(J)

- Nhiệt lượng thu vào của 1 viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:

   Q₂= m₂C₂(0 – t₂) + m₂.λ = 83760(J)

- Số viên nước đá cần phải thả vào nước là:

   705000 : 83760 = 8,4

- Vậy phải thả vào xô ít nhất 9 viên đá để nhiệt độ cuối cùng trong xô là 0°C

Câu 4: Một bình hình trụ, ban đầu chứa mn = 3kg nước ở 24°C. Người ta thả vào bình một cục nước đá có khối lượng mđ = 1,4kg đang ở 0°C. Biết chỉ có nước đá và nước trao đổi nhiệt với nhau; nhiệt dung riêng của nước là C_n = 4200J/kg.K; nhiệt dung riêng của nước đá là Cđ = 1800J/kg.K nhiệt nóng chảy của nước đá là λ= 3,36.10⁵J/kg. Khi có cân bằng nhiệt, hãy tìm nhiệt độ của nước trong bình?

A. 10°C      B. 6°C

C. 1°C      D. 0°C

Hiển thị đáp án

Đáp án: D

- Nhiệt lượng do nước đá thu vào để tan chảy hoàn toàn ở 0°C là:

   Q_thu = mđ.λ = 1,4. 3,36. 10⁵ = 470400 (J)

- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:

   Q_tỏa = mn .C_n.Δt = 3. 4200.( 24 - 0) = 302400 (J)

- Ta thấy Q_thu > Q_tỏa chứng tỏ chỉ 1 phần nước đá bị tan ra.

- Như vậy khi cân bằng nhiệt, hỗn hợp gồm cả nước và nước đá.

- Hay khi cân bằng nhiệt, nhiệt độ của hỗn hợp là t = 0°C.

Câu 5: Một bình nhựa đang có chứa 4 lít nước, dùng nhiệt kế để đo thì xác định được nhiệt độ của nước trong bình là 36°C. Người ta thả vào bình một cục nước đá có khối lượng mđ = 1kg đang ở nhiệt độ -10°C. Biết chỉ có nước đá và nước trao đổi nhiệt với nhau; nhiệt dung riêng của nước là C_n = 4200J/kg.K; nhiệt nóng chảy của nước đá là λ= 3,36.10⁵J/kg. Nhiệt độ của bình khi cân bằng nhiệt là:

A. 0°C      B. -2,1°C

C. 11,9°C      D. 7,3°C

Hiển thị đáp án

Đáp án: C

- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0°C

- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:

   Q_tỏa = mn .C_n.Δt = 4. 4200.(36 - 0) = 604800(J)

- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:

   Q_thu= mđCđ Δt + mđ.λ = 1.1800.10 + 1.3,36.10⁵ = 354000(J)

- Ta thấy Q_thu < Q_tỏa chứng tỏ nước đá bị tan ra hoàn toàn.

- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t°C (t > 0)

- Nhiệt lượng do nước tỏa ra khi hạ xuống 0°C là:

   Q_tỏa = mn .C_n.Δt = 4. 4200.(36 - t) = 604800 -16800.t

- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0°C, tan hết tại 0°C và tăng lên đến t°C là:

   Q_thu= mđCđ Δt + mđ.λ + mn .C_n.(t – 0) = 354000 + 4200.t

   Q_thu = Q_tỏa Suy ra: 604800 -16800.t = 354000 + 4200.t

   ⇒ t = 11,9°C

Câu 6: Một bình kín có chứa 2,5kg nước ở nhiệt độ 25°C. Người ta dẫn 0,5kg hơi nước ở nhiệt độ 100°C vào bình. Biết nhiệt dung riêng và nhiệt hoá hơi của nước lần lượt là C = 4200J/kg.K, L = 2,3.10⁶J/kg. Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài và bình. Tính nhiệt độ sau cùng của hỗn hợp?

Hiển thị đáp án

- Nếu 0,5kg hơi nước ngưng tụ hoàn toàn ở 100°C thì toả ra nhiệt lượng là:

   Q₁ = m₁L = 0,5.2,3.10⁶ = 1150000(J)

- Nếu 2kg nước tăng nhiệt độ đến 100°C thì thu nhiệt lượng là:

   Q₂ = m₂C(t₂ – t₁) = 2,5. 4200.( 100 - 25) = 787500(J)

- Vì Q₂ < Q₁ nên chỉ có một phần hơi nước ngưng tụ và nhiệt độ cân bằng là t = 100°C

Đáp số: 100°C

Câu 7: Người ta dẫn 0,1kg hơi nước ở nhiệt độ 100°C vào một nhiệt lượng kế chứa 2kg nước ở nhiệt độ 25°C. Biết nhiệt dung riêng và nhiệt hoá hơi của nước lần lượt là C = 4200J/kg.K, L = 2,3.10⁶J/kg. Bỏ qua sự trao đổi nhiệt với môi trường bên ngoài. Tính nhiệt độ sau cùng của hỗn hợp?

Hiển thị đáp án

- Nếu 0,1kg hơi nước ngưng tụ hoàn toàn ở 100°C thì toả ra nhiệt lượng là:

   Q₁ = m₁L = 0,1.2,3.10⁶ = 230000(J)

- Nếu 2kg nước tăng nhiệt độ đến 100°C thì thu nhiệt lượng là:

   Q₂ = m₂C(t₂ – t₁) = 2. 4200.( 100 - 25) = 630000(J)

- Vì Q₂ > Q₁ nên hơi nước ngưng tụ hoàn toàn và nhiệt độ cân bằng t < 100°C.

- Nhiệt lượng tỏa ra khi 0,1kg nước hạ từ 100°C xuống t°C là:

   Q₁₁ = m₁C(100 - t)

- Nhiệt lượng thu vào khi 2kg nước tăng từ 25°C đến t°C là:

   Q₂₂ = m₂C(t - 25)

- Áp dụng phương trình cân bằng nhiệt:

   230000 + m₁C(100 - t) = m₂C(t - 25)

⇒ 230000 + 0,1.4200(100 - t) = 2. 4200(t - 25)

⇒ t = 54,65(°C)

Đáp số: 54,65°C

Câu 8: Rót nước ở nhiệt độ t₁ = 20°C vào một nhiệt lượng kế (Bình cách nhiệt). Thả trong nước một cục nước đá có khối lượng m₂ = 0,5kg ở nhiệt độ t₂ = - 15°C. Hãy tìm nhiệt độ của hỗn hợp sau khi cân bằng nhiệt được thiết lập. Biết khối lượng nước đổ vào m₁ = m₂. Cho nhiệt dung riêng của nước C₁ = 4200J/Kgđộ; của nước đá C₂ = 2100J/kg.K; Nhiệt nóng chảy của nước đá λ = 3,4.10⁵J/kg. Bỏ qua khối lượng của nhiệt lượng kế.

Hiển thị đáp án

- Khi được làm lạnh tới 0°C, nước toả ra một nhiệt lượng bằng:

   Q₁ = m₁.C₁(t – 0) = 0,5.4200.20 = 42 000 (J)

- Để làm tăng nhiệt độ nước đá tới 0°C cần tốn một nhiệt lượng:

   Q₂ = m₂.C₂(0 – t₂) = 0,5.2100.15 = 15 750 (J)

- Bây giờ muốn làm cho toàn bộ nước đá ở 0°C tan thành nước cũng ở 0°C cần một nhiệt lượng là:

   Q₃ = λ.m₂ = 3,4.10⁵.0,5 = 170 000J

- Ta thấy:

   Q₁ > Q₂ : Nước đá có thể nóng tới 0°C bằng cách nhận nhiệt lượng do nước toả ra.

   Q₁ < Q₃ + Q₂ : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.

- Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 0°C

Đáp số: 0°C

Câu 9: Thả 1,6kg nước đá ở -10°C vào một nhiệt lượng kế đựng 2kg nước ở 60°C. Bình nhiệt lượng kế bằng nhôm có khối lượng 200g và nhiệt dung riêng là 880J/kg.độ.

a) Nước đá có tan hết không?

b) Tính nhiệt độ cuối cùng của nhiệt lượng kế?

Biết nhiệt dung riêng của nước đá, nhiệt dung riêng của nước, nhiệt nóng chảy của nước đá lần lượt là C_nd = 2100J/kg.độ , C_n = 4190J/kg.độ , λ = 3,4.10⁵J/kg,

Hiển thị đáp án

a) Nhiệt lượng cần cung cấp cho 1,6kg nước đá thu vào để tăng nhiệt độ từ -10°C lên 0°C:

   Q₁ = C₁m₁Δt₁ = C₁m₁ (0 – (-10)) = 2100.1,6.10 = 33600 (J)

- Nhiệt lượng nước đá thu vào để nóng chảy hoàn hoàn ở 0°C

   Q₂ = λm₁ = 3,4.10⁵.1,6 = 5,44.10⁵ = 544000 (J)

- Nhiệt lượng do 2kg nước toả ra để hạ nhiệt độ từ 60°C đến 0°C

   Q₃ = c₂m₂(60 – 0) = 4190.2.60 = 502800 (J)

- Nhiệt lượng do nhiệt lượng kế bằng nhôm toả ra để hạ nhiệt độ từ 60°C xuống tới 0°C

   Q₄ = c₃m₃(60 – 0) = 880.0,2.60 = 10⁵60 (J)

   Q_tỏa = Q₃ + Q₄ = 502800 + 10⁵60 = 513360 (J)

   Q_thu = Q₁+ Q₂ = 33600 + 544000 = 577600 (J)

- Ta thấy: Q_thu > Q_tỏa chứng tỏ nước đá chưa tan hết

b) Nhiệt độ cuối cùng của hỗn hợp nước và nước đá cũng chính là nhiệt độ cuối cùng của nhiệt lượng kế và bằng 0°C

Đáp số: nước đá chưa tan hết. nhiệt độ cuối của hỗn hợp là 0°C

Câu 10: Dẫn 100g hơi nước vào bình cách nhiệt đựng nước đá ở -4°C. Nước đá tan hoàn toàn và lên đến 10°C. Tìm khối lượng nước đá có trong bình. Biết nhiệt nóng chảy của nước đá là λ=3,4.10⁵J/kg, nhiệt hóa hơi của nước là L = 2,3.10⁶J/kg, nhiệt dung riêng của nước là c₁ = 4200J/kg.K , của nước đá là c₂ = 1800J/kg.K.

Hiển thị đáp án

- Nhiệt lượng nước tỏa ra khi ngưng tụ ở 100°C và hạ nhiệt từ 100°C xuống 10°C:

   Q₁ = L.m₁ + m₁.c₁ ( t₁ –t)

- Nhiệt lượng nước đá thu vào để tăng nhiệt độ từ -4°C đến 0°C sau đó nóng chảy hoàn toàn thành nước ở 0°C và tăng nhiệt độ từ 0°C đến 10°C:

   Q₂ = m₂.c₂. ( t₃ – t₂) + m₂.λ+ m₂.c₁.( t –t₃)

- Theo phương trình cân bằng nhiệt, ta có:

   L.m₁ + m₁.c₁.(t₁ –t) = m₂ [c₂( t₃ – t₂) + λ + c₁.(t –t₃)]