Khám phá 2 trang 35 Chuyên đề Toán 10

Giải Chuyên đề Toán 10 Bài 2: Nhị thức Newton

Haylamdo biên soạn và sưu tầm lời giải Khám phá 2 trang 35 Chuyên đề Toán 10 trong Bài 2: Nhị thức Newton. Với lời giải chi tiết nhất hy vọng sẽ giúp học sinh biết cách làm bài tập Chuyên đề Toán 10.

Khám phá 2 trang 35 Chuyên đề Toán 10: Từ các công thức khai triển:

(a + b)⁰ = 1;

(a + b)¹ = a + b;

(a + b)² = a² + 2ab + b²;

(a + b)³ = a³ + 3a²b + 3ab² + b³;

(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴;

(a + b)5 = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵;

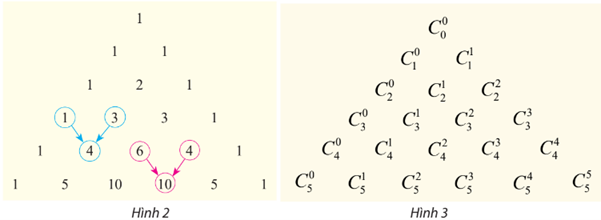
các hệ số được viết thành bảng số như Hình 2 sau đây. Nếu sử dụng kí hiệu tổ hợp thì nhận được bảng như Hình 3.

Từ các đẳng thức như

$\begin{array}{cccccccccccccccccccc}{C}_3^0=C_3^3=1,& C_4^1=C_4^3=4,& & & & & & & & & & & & & & & & & & \\ C_3^0+C_3^1=C_4^1,& C_4^2+C_4^3=C_5^3,& & & & & & & & & & & & & & & & & & \end{array}$

có thể dự đoán rằng, với mỗi $n\in {\mathrm{\mathbb{N}}}^{*}$

$C_n^k=C_n^{n-k}(0\le k\le n);$

$C_n^{k-1}+C_n^k=C_{n+1}^k(1\le k\le n).$

Hãy chứng minh các công thức trên.

Gợi ý: Sử dụng công thức $C_n^k=\frac{n!}{k!(n-k)!},n\in \mathrm{\mathbb{N}},0\le k\le n.$

Lời giải:

+) Có $C_n^k=\frac{n!}{k!(n-k)!},C_n^{n-k}=\frac{n!}{(n-k)![n-(n-k)]!}=\frac{n!}{(n-k)!k!}=\frac{n!}{k!(n-k)!}.$

Vậy $C_n^k=C_n^{n-k}.$

+) $C_n^{k-1}+C_n^k=\frac{n!}{(k-1)!(n-k+1)!}+\frac{n!}{k!(n-k)!}$

$=\frac{\frac{(n+1)!}{n+1}}{\frac{k!}{k}(n-k+1)!}+\frac{\frac{(n+1)!}{n+1}}{k!\frac{(n-k+1)!}{(n-k+1)}}=\frac{k}{n+1}.\frac{(n+1)!}{k!(n-k+1)!}+\frac{n-k+1}{n+1}.\frac{(n+1)!}{k!(n-k+1)!}$

$=\frac{k}{n+1}.\frac{(n+1)!}{k![(n+1)-k]!}+\frac{n-k+1}{n+1}.\frac{(n+1)!}{k![(n+1)-k]!}$

$=\frac{k}{n+1}.C_{n+1}^k+\frac{n-k+1}{n+1}.C_{n+1}^k=(\frac{k}{n+1}+\frac{n-k+1}{n+1})C_{n+1}^k$

$=\frac{k+(n-k+1)}{n+1}{C}_{n+1}^k=\frac{n+1}{n+1}{C}_{n+1}^k=C_{n+1}^k.$