Bài 1 trang 134 Toán 9 Tập 2

Bài tập ôn cuối năm (Phần Đại Số - Phần Hình Học)

Bài 1 trang 134 Toán 9 Tập 2: Chu vi của hình chữ nhật ABCD là 20cm. Hãy tìm giá trị nhỏ nhất của độ dài đường chéo AC.

Bài giải:

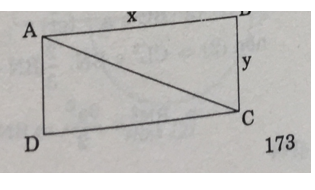
Gọi x và y là hai kích thước của hình chữ nhật (x > 0; y > 0)

Ta có: x+y = 10 (cm)     (1)

và 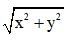= độ dài đường chéo

mà (x + y)² = x² + 2xy + y²

⇔ x² + y² = 100 – 2xy (do (1))     (2)

Nên (2) cho: 100 – 2xy ≥ 2xy ⇒ xy ≤ 25

⇒ giá trị lớn nhất của xy là 25.

Suy ra giá trị nhỏ nhất của x² + y² là 100 – 2.25 = 50

Vậy giá trị nhỏ nhất của đường chéo là √50 hay 5√2 cm.

Cách khác:

Đặt x = AB (x > 0) và y = BC (y > 0) ta có: x + y = 10 (cm)

Đường chéo AC =

Mà x² + y² = (x² + y²) – 2xy ⇔ x² + y² = 100 – 2xy

Do đó x² + y² nhỏ nhất ⇔ xy lớn nhất. Mà tổng x + y = 10 (không đổi) nên xy lớn nhất ⇔ x = y. Suy ra x = y = 5

Vậy x² + y² lớn nhất ⇔ x² + y² = 50

⇔ giá trị nhỏ nhất của đường chéo là √50 hay 5√2 cm.