Bài 15 trang 135 Toán 9 Tập 2

Bài tập ôn cuối năm (Phần Đại Số - Phần Hình Học)

Bài 15 trang 135 Toán 9 Tập 2: Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và AB ở D và E. Chứng minh:

a) BD² = AD.CD

b) Tứ giác BCDE là tứ giác nội tiếp

c) BC // DE.

Bài giải:

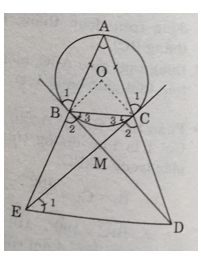
b) Ta có: sđ cung AB = sđ cung AC (do AB = AC)

⇒ góc B₁ = góc C₁ ⇒ góc B₂ = góc C₂

Hai điểm B và C cùng nhìn đoạn BC dưới hai góc bằng nhau nên B và C nằm trên cung chứa góc B₂ = góc C₂ dựng trên đoạn BC.

Do đó BDCE là tứ giác nội tiếp

c) Gọi M là giao điểm của BD và CE ta có:

ΔMBC cân tại M ⇒ góc B₃ = góc C₃

mà góc B₃ = góc E₃ (góc nội tiếp cùng chắn cung CD) ⇒ góc E₃ = góc C₃

Do đó BC // DE.