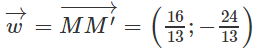đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d1 có phương trình 2x − 3y − 5 = 0
Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến
Bài 1.2 trang 10 Sách bài tập Hình học 11: Trong mặt phẳng v→ = (−2;1) cho, đường thẳng d có phương trình 2x − 3y + 3 = 0, đường thẳng d1 có phương trình 2x − 3y − 5 = 0.
a) Viết phương trình của đường thẳng d’ là ảnh của d qua Tv→.
b) Tìm tọa độ của w→ có giá vuông góc với đường thẳng d để d1 là ảnh của d qua Tw→.
Lời giải:
a) Lấy một điểm thuộc d, chẳng hạn M = (0; 1).
Khi đó M′ = Tv→(M) = (0 − 2; 1 + 1) = (−2; 2) thuộc d'. Vì d' song song với d nên phương trình của nó có dạng 2x − 3y + C = 0. Do M' ∈ d′ nên 2.(−2) − 3.2 + C = 0. Từ đó suy ra C = 10 . Do đó d' có phương trình 2x − 3y + 10 = 0.
b) Lấy một điểm thuộc d, chẳng hạn M = (0; 1). Đường thẳng d2 qua M vuông góc với có vectơ chỉ phương là v→ = (2; −3). Do đó phương trình của d2 là
. Gọi M' là giao của d1 với d2 thì tọa độ của nó phải thỏa mãn hệ phương trình:
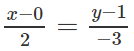
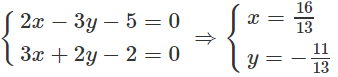
Từ đó suy ra
