Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x^2 + y^2 − 2x + 4y – 4 = 0

Bài 1: Phép biến hình - Bài 2: Phép tịnh tiến

Bài 1.4 trang 10 Sách bài tập Hình học 11: Trong mặt phẳng Oxy cho đường tròn (C) có phương trình x² + y² − 2x + 4y – 4 = 0. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ v→ = (−2;5).

Lời giải:

Cách 1. Dễ thấy (C) là đường tròn tâm I(1; −2), bán kính r = 3. Gọi I′ = T_v→(I) = (1 − 2; −2 + 5) = (−1;3) và (C') là ảnh của (C) qua T_v→ thì (C') là đường tròn tâm (I') bán kính r = 3. Do đó (C') có phương trình: (x + 1)² + (y − 3)² = 9.

Cách 2. Biểu thức tọa độ của T_v→ là

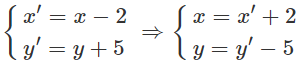
Thay vào phương trình của (C) ta được

(x′ + 2)² + (y′ − 5)² − 2(x′ + 2) + 4(y′ − 5) – 4 = 0

⇔ x′² + y′² + 2x′ − 6y′ + 1 = 0

⇔ (x′ + 1)² + (y′ − 3)² = 9

Do đó (C') có phương trình (x + 1)² + (y − 3)² = 9