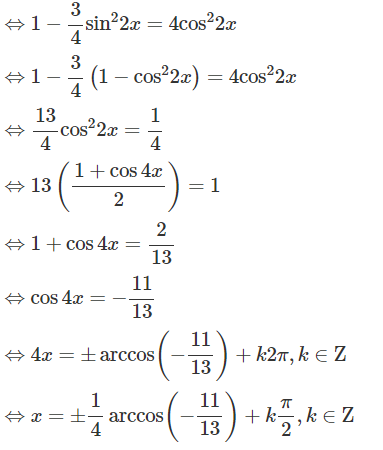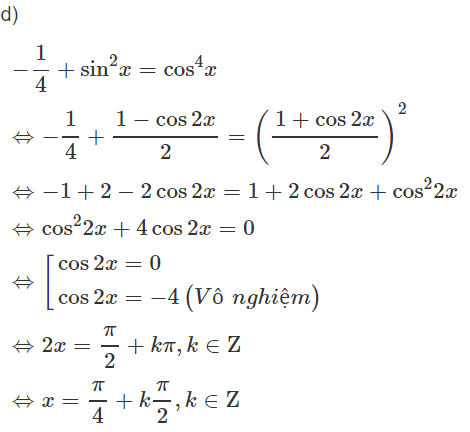Giải các phương trình sau 3cos^2x - 2sinx + 2 = 0

Bài 3: Một số phương trình lượng giác thường gặp

Bài 1.26 trang 37 Sách bài tập Đại số 11: Giải các phương trình sau

a) 3cos²x - 2sinx + 2 = 0

b) 5sin²x + 3cosx + 3 = 0

c) sin⁶x + cos⁶x = 4cos²2x

d) -0,25 + sin²x = cos⁴x

Lời giải:

a) 3cos²x - 2sinx + 2 = 0

⇔ 3(1 - sin²x) - 2sinx + 2 = 0

⇔ 3sin²x + 2sinx - 5 = 0

⇔ (sinx - 1)(3sinx + 5) = 0

⇔ sinx = 1

⇔ x = π/2 + k2π, k ∈ Z

b) 5sin²x + 3cosx + 3 = 0

⇔ 5(1 - cos²x) + 3cosx + 3 = 0

⇔ 5cos²x - 3cosx - 8 = 0

⇔ (cosx + 1)(5cosx - 8) = 0

⇔ cosx = -1

⇔ x = (2k + 1)π, k ∈ Z

c) sin⁶x + cos⁶x = 4cos²2x

⇔ (sin²x + cos²x)³ - 3sin²x.cos²x(sin²x + cos²x) = 4cos²2x