Giải các phương trình sau 2tanx - 3cotx - 2 = 0

Bài 3: Một số phương trình lượng giác thường gặp

Bài 1.27 trang 37 Sách bài tập Đại số 11: Giải các phương trình sau

a) 2tanx - 3cotx - 2 = 0;

b) cos²x = 3sin2x + 3;

c) cotx - cot2x = tanx + 1.

Lời giải:

a) 2tanx - 3cotx - 2 = 0 (Điều kiện cosx ≠ 0 và sinx ≠ 0)

Ta có

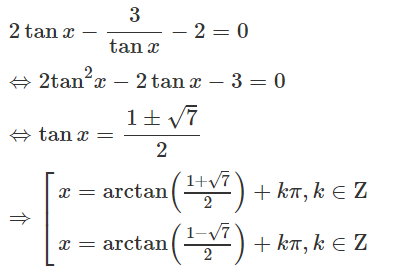
Các giá trị này thỏa mãn điều kiện nên là nghiệm của phương trình

b) cos²x = 3sin2x + 3

Ta thấy cosx = 0 không thỏa mãn phương trình. Với cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:

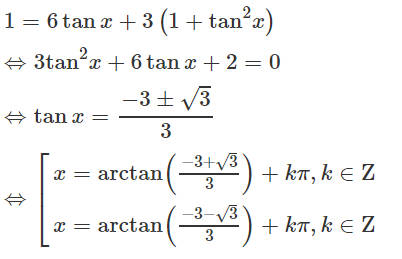
c) cotx - cot2x = tanx + 1 (1)

Điều kiện: sinx ≠ 0 và cosx ≠ 0. Khi đó:

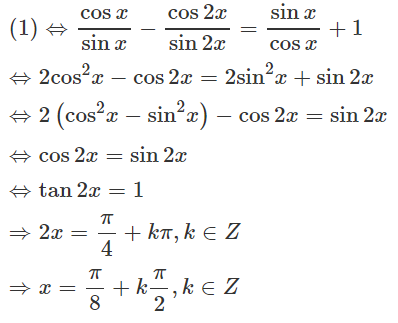
Các giá trị này thỏa mãn điều kiện nên là nghiệm của phương trình