(SGK + SBT) Giải Toán 11 trang 38 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
Haylamdo giới thiệu lời giải bài tập Toán 11 trang 38 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 38.
(SGK + SBT) Giải Toán 11 trang 38 Kết nối tri thức, Chân trời sáng tạo, Cánh diều
- Toán lớp 11 trang 38 Tập 1 (sách mới):
- Toán lớp 11 trang 38 Tập 2 (sách mới):
Lưu trữ: Giải Toán 11 trang 38 (sách cũ)
Bài 1.30 trang 38 Sách bài tập Đại số 11: Giải các phương trình sau:
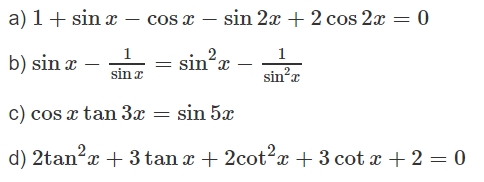
Lời giải:
a) 1 + sinx - cosx - sin2x + 2cos2x = 0 (1)
Ta có:
1 - sin2x = (sinx - cosx)2
⇔ 2cos2x = 2(cos2x - sin2x) = -2(sinx - cosx)(sinx + cosx)
Vậy (1) ⇔ (sinx - cosx)(1 + sinx - cosx - 2sinx - 2cosx) = 0
⇔ (sinx - cosx)(1 - sinx - 3cosx) = 0
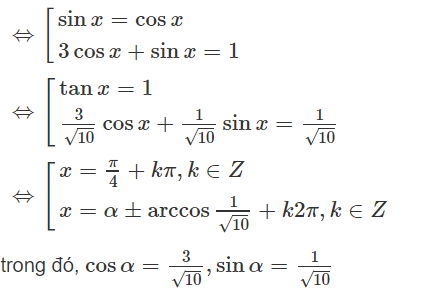
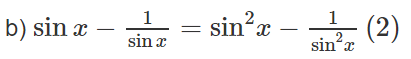
Điều kiện sinx ≠ 0
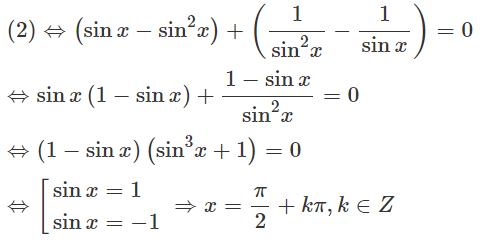
(thỏa mãn điều kiện)
c) cosx.tan3x = sin5x
Điều kiện: cos3x ≠ 0. Khi đó,
(3)⇔ cosx.sin3x = cos3x.sin5x
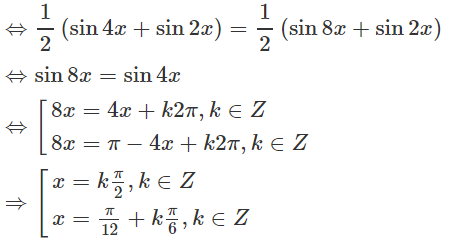
Kết hợp với điều kiện ta được nghiệm của phương trình là:
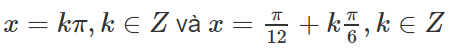
d) 2tan2x + 3tanx + 2cot2x + 3cotx + 2 = 0 (4)
Điều kiện: cosx ≠ 0 và sinx ≠ 0. Khi đó,
(4) ⇔ 2(tan2x + cot2x) + 3(tanx + cotx) + 2 = 0 ⇔ 2[(tanx + cotx)2 − 2] + 3(tanx + cotx) + 2 = 0
Đặt t = tanx + cotx ta được phương trình
2t2 + 3t − 2 = 0 ⇒ t = −2, t = 0,5
Với t = -2 ta có tanx + cotx = -2
⇔ tan2x + 2tanx + 1 = 0 ⇒ tanx = −1 ⇒ x = −π/4 + kπ, k ∈ Z
(thỏa mãn điều kiện)
Với t = 0,5 ta có tanx + cotx = 0,5 ⇔ 2tan2x − tanx + 2 = 0
Phương trình này vô nghiệm.
Vậy nghiệm của phương trình (4) là x = −π/4 + kπ,k ∈ Z

