Nghiệm của phương trình 3cotx - √3 = 0 là

---

Bài 3: Một số phương trình lượng giác thường gặp

Bài 1.32: Nghiệm của phương trình 3cotx - √3 = 0 là:

Lời giải:

Ta có cotx = 1/√3 ⇒ x = π/3+ kπ, k ∈ Z.

Chọn đáp án: B

Bài 1.33: Nghiệm của phương trình sin⁴x - cos⁴x = 0 là

Lời giải:

Ta có sin⁴ x - cos⁴ x = 0 ⇔ (sin² x + cos²x)( sin² x- cos² x) = 0

⇔ sin² x – cos²x = 0 ⇔ cos2x = 0 ⇔ 2x = π/2 + kπ ⇔ x = π/4 + kπ/2.

Chọn đáp án: C

Bài 1.34: Cho phương trình 4cos²2x + 16sinx.cosx - 7 = 0 (1)

Xét các giá trị

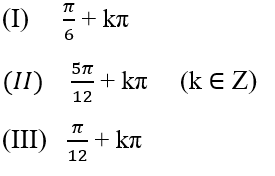
Trong các giá trị trên, giá trị nào là nghiệm của phương trình (1) ?

A. Chỉ (I)            B. Chỉ (II)

C. Chỉ (III)            D. Chỉ (II) và (III)

Lời giải:

Ta có (1) ⇔ 4(1 - sin² 2x) + 8sin2x – 7 = 0 ⇔ 4sin² 2x – 8sin2x + 3 = 0

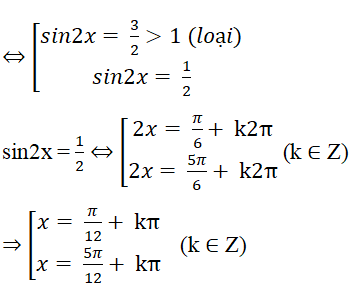
Chọn đáp án: D

Bài 1.35: Nghiệm của phương trình cosx.cos7x = cos3x.cos5x là

Lời giải:

Ta có: cosx.cos7x = cos3x.cos5x

⇔ cos8x + cos6x = cos8x + cos2x ⇔ cos6x = cos2x ⇔ 6x = ±2x + k2π.

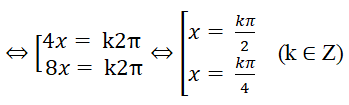
Vì tập hợp giá trị kπ/4 bao tập các giá trị kπ/2 nên nghiệm của phương trình là kπ/4, k ∈ Z.

Chọn đáp án:

Bài 1.36: Nghiệm của phương trình 3tan2x + 6cotx = -tanx là

Lời giải:

Điều kiện của phương trình:

x ≠ kπ, x ≠ π/2 + kπ, x ≠ π/4 + kπ/2 (k ∈ Z)

Xét các phương án.

- Vì π/4 và π/2 không thỏa mãn điều kiện của phương trình nên hai phương án A và D bị loại.

- Với x = π/6 thì vế phải của phương trình đã cho âm, còn vế trái dương, nên phương án C bị loại.

Chọn đáp án: B

Bài 1.37: Nghiệm của phương trình 2sinx = 3cotx là

Lời giải:

Điều kiện của phương trình: x ≠ kπ (k ∈ Z)

Cách 1. Giải trực tiếp.

Biến đổi phương trình đã cho ta được

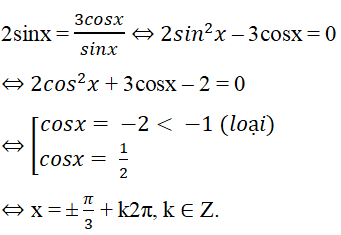
Cách 2. Xét các phương án.

- Với x = π/6 thì vế trái của phương trình bằng 1, còn vế phải là 3√3 nên phương án A bị loại.

- Giá trị kπ/2 với k = 2 không thỏa mãn điều kiện của phương trình nên phương án B bị loại.

- Với x = π/4 thì vế trái của phương trình bằng √2, còn vế phải bằng 3, nên phương án C bị loại.

Chọn đáp án: D

Bài 1.38: Cho phương trình √3.cosx + sinx = 2(∗)

Xét các giá trị

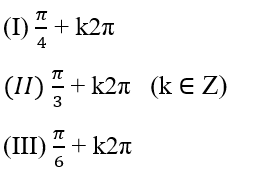
Trong các giá trị trên, giá trị nào là nghiệm của phương trình (∗)

A. Chỉ (I)            B. Chỉ (II)

C. Chỉ (III)            D. Chỉ (I) và (III)

Lời giải:

Ta có (*) ⇔ 2(√3/2 cosx+ 1/2 sinx) = 2

⇔ cos(x- π/6) = 1 ⇔ x = π/6 + k2π, k ∈ Z.

Chọn đáp án: C