Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC

Câu hỏi ôn tập chương 1

Bài 1.33 trang 37 Sách bài tập Hình học 11: Cho tam giác ABC. Tìm một điểm M trên cạnh AB và một điểm N trên cạnh AC sao cho MN song song với BC và AM = CN.

Lời giải:

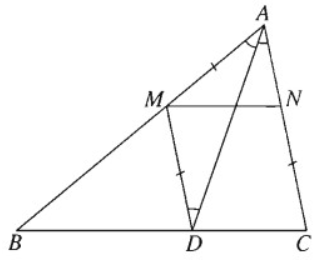
Giả sử đã dựng được hai điểm M, N thỏa mãn điều kiện đầu bài. Đường thẳng qua M và song song với AC cắt BC tại D. Khi đó tứ giác MNCD là hình bình hành. Do đó CN = DM. Từ đó suy ra tam giác AMD cân tại M. Do đó . Suy ra AD là phân giác trong của góc A. Do đó AD dựng được .Ta lại có NM→ = CD→, nên có thể xem M là ảnh của N qua phép tịnh tiến theo vectơ DC→.

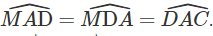
Từ đó suy ra cách dựng:

- Dựng đường phân giác trong của góc A. Đường này cắt BC tại D.

- Dựng đường thẳng d là ảnh của đường thẳng AC qua phép tịnh tiến theo vectơ CD→. d cắt AB tại M.

- Dựng N sao cho NM→ = CD→.

Khi đó dễ thấy M, N thỏa mãn điều kiện đầu bài.