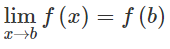Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c)

Bài 3: Hàm số liên tục

Bài 4.34 trang 171 Sách bài tập Đại số 11: Chứng minh rằng nếu một hàm số liên tục trên (a; b] và trên [b; c) thì nó liên tục trên (a; c)

Lời giải:

Vì hàm số liên tục trên (a; b] nên liên tục trên (a; b) và

(1)

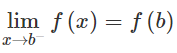
Vì hàm số liên tục trên [b; c) nên liên tục trên (b; c) và

(2)

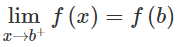
Từ (1) và (2) suy ra f(x) liên tục trên các khoảng (a; b), (b; c) và liên tục tại x = b (vì ). Nghĩa là nó liên tục trên (a; c)