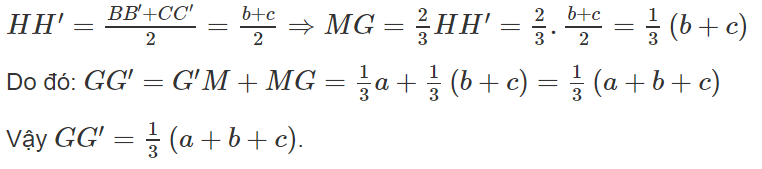Giải Toán 11 trang 81 Kết nối tri thức, Chân trời sáng tạo
Haylamdo giới thiệu lời giải bài tập Toán 11 trang 81 Kết nối tri thức, Chân trời sáng tạo sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 81.
Giải Toán 11 trang 81 Kết nối tri thức, Chân trời sáng tạo
- Toán lớp 11 trang 81 Tập 1 (sách mới):
- Toán lớp 11 trang 81 Tập 2 (sách mới):
Lưu trữ: Giải Toán 11 trang 81 (sách cũ)
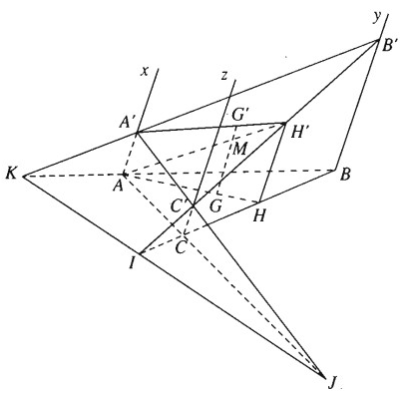
Bài 2.37 trang 81 Sách bài tập Hình học 11: Trong mặt phẳng (α) cho tam giác ABC. Từ ba đỉnh của tam giác này ta kẻ các nửa đường thẳng song song cùng chiều Ax, By, Cz không nằm trong (α). Trên Ax lấy đoạn AA' = a, trên By lấy đoạn BB' = b, trên Cz lấy đoạn CC' = c.
a) Gọi I, J và K lần lượt là các giao điểm B'C', C'A' và A'B' với (α).
Chứng minh rằng
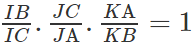
b) Gọi G và G' lần lượt là trọng tâm của các tam giác ABC và A'B'C'.
Chứng minh: GG′ // AA′.
c) Tính GG' theo a, b, c
Lời giải:
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
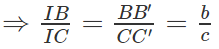
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
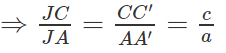
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
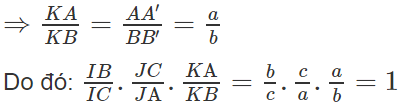
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
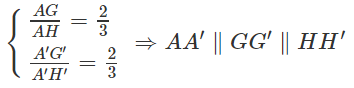
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
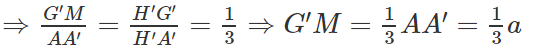
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
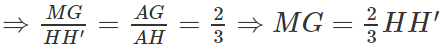
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên