Lập dãy số (Vn) với vn = Un + 1 − Un. Chứng minh dãy số (Un) là cấp số cộng

Ôn tập chương 3

Bài 3.40 trang 133 Sách bài tập Đại số 11: Cho dãy số

(u_n):

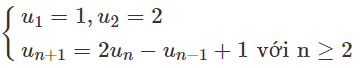
a) Viết năm số hạng đầu của dãy số ;

b) Lập dãy số (v_n) với v_n = u_n + 1 − u_n. Chứng minh dãy số (vn) là cấp số cộng ;

c) Tìm công thức tính (u_n) theo n.

Lời giải:

a) Năm số hạng đầu là 1, 2, 4, 7, 11

b) Từ công thức xác định dãy số ta có

u_n+1 = 2u_n – u_n-1 + 1 hay u_n+1 − u_n = u_n − u_n−1 + 1 (1)

Vì v_n = u_n+1 − u_n nên từ (1), ta có

v_n = v_n−1 + 1 với n ≥ 2 (2)

Vậy (v_n) là cấp số cộng với v₁ = u₂ − u₁ = 1 công sai d = 1

c) Để tính (u_n) ta viết