Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng

Câu hỏi ôn tập chương 1

Bài 1.40 trang 38 Sách bài tập Hình học 11: Gọi A’, B’ và C’ tương ứng là ảnh của ba điểm A, B và C qua phép đồng dạng. Chứng minh rằng nếu AB→ = pAC→ thì A'B'→ = pA'C'→, trong đó p là một số. Từ đó chứng minh rằng phép đồng dạng biến ba điểm thẳng hàng thành ba điểm thẳng hàng và nếu điểm B nằm giữa hai điểm A và C thì điểm B' nằm giữa hai điểm A’ và C’.

Lời giải:

Để ý rằng

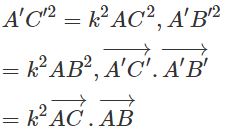
Ta có:

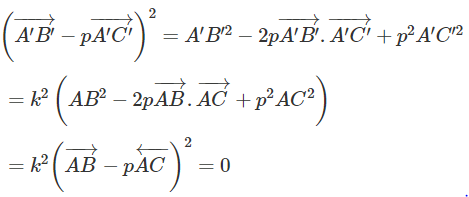
Từ đó suy ra

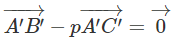
Giả sử ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Khi đó AB→ = tAC→, với 0 < t < 1. Áp dụng bài 1.39 ta cũng có A'B→ = tA'C'→, với 0 < t < 1. Do đó ba điểm A′, B′, C′ thẳng hàng và điểm B' nằm giữa hai điểm A' và C'.