Bằng phép thử ta có P(1), P(2), P(3), P(4) là đúng. Khẳng định nào sau đây là sai

Bài 1: Phương pháp quy nạp toán học

Bài tập trắc nghiệm trang 107, 108 Sách bài tập Đại số 11:

Bài 3.7: Xét mệnh đề chứa biến P(n): "10^{n - 1} < n + 2017 với n ∈ N^∗"

Bằng phép thử ta có P(1), P(2), P(3), P(4) là đúng. Khẳng định nào sau đây là sai?

A. P(n) đúng với mọi số chẵn n ≤ 4             B. P(n) đúng với mọi số lẻ n < 4

C. P(n) đúng với mọi số n             D. P(n) đúng với mọi số n ≤ 4

Lời giải:

Vì các phương án A; B; D là đúng nên phương án C là sai. Mặt khác cũng có thể thấy C sai cả về hai phương diện suy luận (việc thử với n = 1, 2, 3, 4 không phải là chứng minh) và thực tế (dễ thấy P(5) là sai, tổng quát ta có thể chứng minh 10^(n-1) > n + 2017 với n ≥ 5)

Chọn đáp án: C

Bài 3.8: Đặt . Giả sử hệ thức là đúng với n = k ≥ 1. Để chứng minh hệ thức trên cũng đúng với n = k + 1, ta phải chứng minh S_{k + 1} bằng:

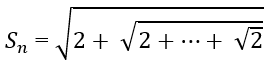
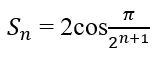
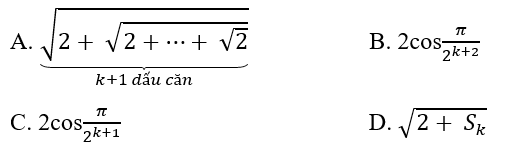
Lời giải:

Chọn đáp án: B