Cho khối hộp ABCD.A’B’C’D’. Chứng minh rằng sáu trung điểm của sáu cạnh AB, BC, CC’, C’D’, D’A’ và A’A

Ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 2 trang 31 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 2 (trang 31 sgk Hình Học 12 nâng cao): Cho khối hộp ABCD.A’B’C’D’. Chứng minh rằng sáu trung điểm của sáu cạnh AB, BC, CC’, C’D’, D’A’ và A’A nằm trên một mặt phẳng và mặt phẳng đó chia khối hộp thành hai phần có thể tích bằng nhau.

Lời giải:

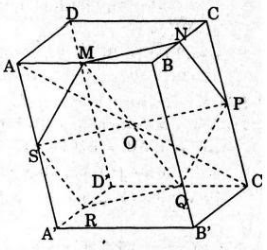
Gọi O là giao điểm của các đường chéo của hình hộp. Ta có O là trung điểm của AC’, tứ giác AMC’Q là hình bình hành nên O là trung điểm của MQ.

Vậy O, M, Q thẳng hàng. Hơn nữa MN, SP, RQ đôi một song song và lần lượt đi qua O, M, Q nên M, N, P, Q, R, S cùng nằm trên mp(α) đi qua O (và mp(α) // (ACD’)).

Ta thấy O là trung điểm của AC’, BD’, A’C, B’D, MQ, NR, SP nên (α) chia khối hộp thành hai phần là ảnh của nhau qua V^(O,-1) (hay phép đối xứng tâm O). Do đó chúng có thể tích bằng nhau.