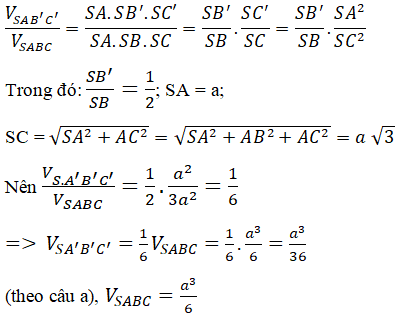Cho khối chóp S.ABC có đường cao SA = a, đáy là tam giác vuông cân AB=BC = a

Ôn tập chương 1

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 31 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 6 (trang 31 sgk Hình Học 12 nâng cao): Cho khối chóp S.ABC có đường cao SA = a, đáy là tam giác vuông cân AB=BC = a. Gọi B’ là trung điểm của SB, C’ là chân đường cao hạ từ A của ∆SAC.

a) Tính thể tích khối chóp S.ABC

b) Chứng minh rằng SC ⊥ (AB’C’)

c) Tính thể tích khối chóp S.AB’C’

Lời giải:

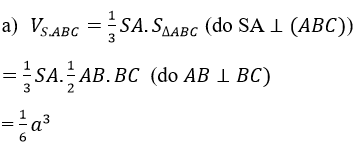
b) Cách 1. Ta có: BC⊥AB (gt)

BC⊥SA (do SA⊥(ABC))

=>BC⊥(SAB)=>SB là hình chiếu của SC trên (SAB)

Mặt khác: SA = AB (do đều bằng a) và B’ là trung điểm của SB nên AB'⊥SB . vậy AB'⊥SC (1) (định lí 3 đường vuông góc)

Lại có, C’ là hình chiếu của A trên SC nên AC’⊥ SC (2)

Từ (1), (2) suy ra SC⊥(AB'C')

Cách 2.

Ta có: BC ⊥(SAB) vì (BC ⊥AB,BC⊥SA do SA ⊥(SAB) => BC ⊥AB'

Lại có SB ⊥AB'(trung tuyến trong tam giác cân)

Vậy AB’ ⊥(SBC)=> AB'⊥SC (1)

Mặt khác C’ là hình chiếu của A trên SC nên AC’ ⊥ SC (2)

Từ (1), (2) suy ra SC ⊥(AB'C' )

c) Tính V_S.AB'C'?

Cách 1. Vì SC'⊥AB'C' nên:

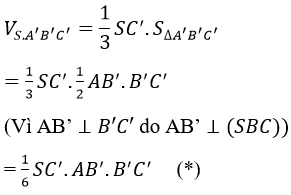
(trung tuyến trong tam giác vuông)

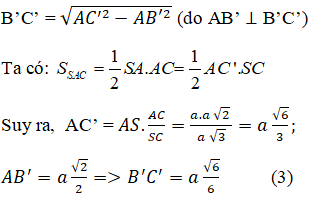
Thay (1), (2), (3) vào (*) ta được:

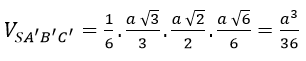
Nhận xét:

Ta có: AB'⊥(SBC) nên có thể lấy V = (1/3)AB'.S_ΔSB'C'=(1/6). AB'.B' C'.SC' rồi giải như cách 1.

Cách 2: ta có: