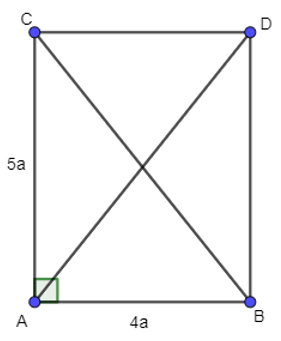
Cho tam giác ABC vuông tại A, AB = 4a, AC = 5a. Tính a) | vectơ AB - vectơ AC |

Cho tam giác ABC vuông tại A, AB = 4a, AC = 5a. Tính:

Giải sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ

Bài 38 trang 92 SBT Toán 10 Tập 1: Cho tam giác ABC vuông tại A, AB = 4a, AC = 5a. Tính:

a) $|\overrightarrow{AB}-\overrightarrow{AC}|$ ;

b) $|\overrightarrow{AB}+\overrightarrow{AC}|$ .

Lời giải:

a) Xét tam giác ABC vuông tại A, có:

BC² = AB² + AC² (định lí pythagoras)

⇔ BC² = (4a)² + (5a)² = 41a²

⇔ BC = $\sqrt{41}$ a.

Ta có: $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{CA}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CB}$

⇒ $|\overrightarrow{AB}-\overrightarrow{AC}|=|\overrightarrow{CB}|=\sqrt{41}a$ .

Vậy $|\overrightarrow{AB}-\overrightarrow{AC}|=\sqrt{41}a$ .

b) Lấy điểm D là điểm thỏa mãn ABDC là hình chữ nhật nên AD = BC (tính chất hình hình chữ nhật).

Ta có: $\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$ (quy tắc hình bình hành)

⇒ $|\overrightarrow{AB}+\overrightarrow{AC}=|\overrightarrow{AD}=|\overrightarrow{CB}=\sqrt{41}a$ .

Vậy $|\overrightarrow{AB}+\overrightarrow{AC}|=\sqrt{41}a.$