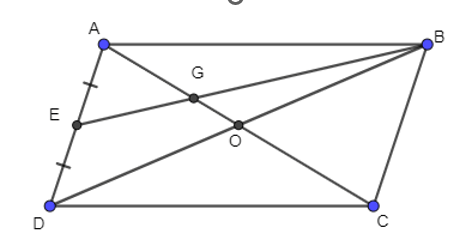
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo, E là trung điểm của AD

Giải sách bài tập Toán 10 Bài 4: Tổng và hiệu của hai vectơ

Bài 43 trang 93 SBT Toán 10 Tập 1: Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo, E là trung điểm của AD, G là giao điểm của BE và AC. Tính:

a) $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}$ ;

b) $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GD}$ .

Lời giải:

a) Xét hình bình hành ABCD, có O là giao điểm của AC và BD nên O là trung điểm của AC và O là trung điểm của BD.

⇒ $\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}$ và $\overrightarrow{OB}+\overrightarrow{OD}=\overrightarrow{0}$

Ta có: $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}$

$=\left(\overrightarrow{OA}+\overrightarrow{OC}\right)+\left(\overrightarrow{OB}+\overrightarrow{OD}\right)$.

$=\overrightarrow{0}+\overrightarrow{0}$$=\overrightarrow{0}$

Vậy $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$ .

b) Xét tam giác ABD, có:

AO là trung tuyến, BE là đường trung tuyến

Mà AO giao với BE tại G nên G là trọng tâm tam giác ABD

⇒ $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GD}=\overrightarrow{0}$

Vậy $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GD}=\overrightarrow{0}$ .