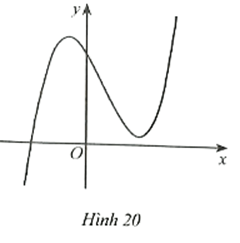
Cho hàm số y = ax^3 + bx^2 + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20

Cho hàm số y = ax + bx + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20.

Giải SBT Toán 12 Cánh diều Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 76 trang 37 SBT Toán 12 Tập 1: Cho hàm số y = ax³ + bx² + cx + d (a ≠ 0) có đồ thị là đường cong ở Hình 20.

a) a > 0.
b) Đồ thị cắt trục tung tại điểm có tung độ dương.
c) Đồ thị hàm số có hai điểm cực trị nằm cùng phía với trục tung.
d) b < 0.

Lời giải:

a) Đ

b) Đ

c) S

d) S

Căn cứ vào hình dáng của đồ thị hàm số, ta có a > 0.

Đồ thị cắt trục tung tại điểm (0; d) nằm phía trên trục hoành nên điểm này có tung độ dương.

Đồ thị hàm số có hai điểm cực trị nằm ở hai phía trục tung.

Ta có: y = ax³ + bx² + cx + d ⇒y' = 3ax² + 2bx + c

Hàm số có hai cực trị nên y' = 0 có hai nghiệm phân biệt x₁, x₂.

Theo Viet ta có: x₁ + x₂ = $\frac{- 2 b}{3 a}$ .

Ta thấy trung điểm đoạn nối hai điểm cực trị x₁, x₂ nằm về phía bên phải trục tung nên tổng hai điểm cực trị x₁, x₂ dương hay $\frac{- 2 b}{3 a}$ > 0.

Mà a > 0 nên b < 0.

Lời giải SBT Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯