Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

❮ Bài trước Bài sau ❯

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

Giải SBT Toán 12 Cánh diều Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số

Bài 81 trang 38 SBT Toán 12 Tập 1: Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau:

a) y = $\frac{2 x - 1}{x + 1}$ ;

b) y = $\frac{x}{x - 2}$ ;

c) y = $\frac{x^{2} - 2 x + 2}{- x + 1}$ ;

d) y = $\frac{x^{2} + 2 x - 3}{x + 2}$ .

Lời giải:

a) y = $\frac{2 x - 1}{x + 1}$

1) Tập xác định: D = ℝ\{−1}.

2) Sự biến thiên.

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.

Ta có: $\lim_{x \to + \infty}$ y = 2, $\lim_{x \to - \infty}$ y = 2.

Do đó, đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

$\lim_{x \to - 1^{-}}$ y = +∞, $\lim_{x \to - 1^{+}}$ y = −∞.

Do đó, đường thẳng x = −1 là tiệm cận đứng của đồ thị hàm số.

Ta có: y' = $\frac{3}{{(x + 1)}^{2}}$ > 0, với ∀x ∈ D.

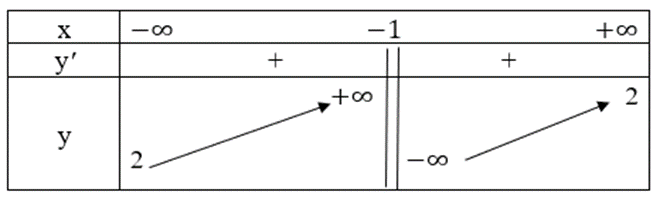
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Hàm số đồng biến trên các khoảng (−∞; −1) và (−1; +∞).

3) Đồ thị:

Đồ thị hàm số nhận đường thẳng x = −1 là tiệm cận đứng, y = 2 là tiệm cận ngang.

Giao của đồ thị với trục tung tại điểm (0; −1), giao của đồ thị với trục hoành tại điểm $(\frac{1}{2}; 0)$ .

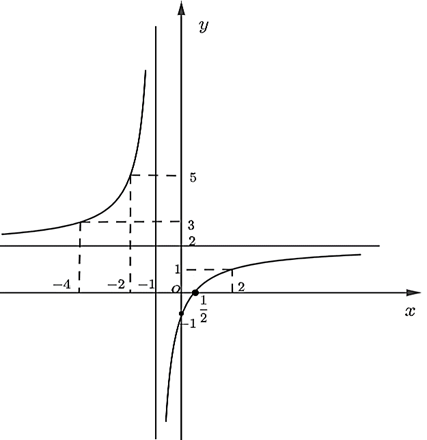
Đồ thị hàm số đi qua các điểm: (−4; 3); (−2; 5); (2; 1); $(\frac{1}{2}; 0)$ ; (0; −1).

Ta có đồ thị như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−1; 2) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

b) y = $\frac{x}{x - 2}$

1) Tập xác định: D = ℝ\{2}.

2) Sự biến thiên.

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.

Ta có: $\lim_{x \to + \infty}$ y = 1, $\lim_{x \to - \infty}$ y = 1.

Do đó, đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

$\lim_{x \to 2^{-}}$ y = −∞, $\lim_{x \to 2^{+}}$ y = +∞.

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

Ta có: y' = $\frac{- 2}{{(x - 2)}^{2}}$ < 0, với ∀x ∈ D.

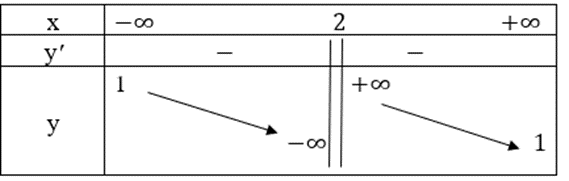
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Hàm số nghịch biến trên các khoảng (−∞; 2) và (2; +∞).

3) Đồ thị

Đồ thị hàm số nhận đường thẳng x = 2 làm tiệm cận đứng và y = 1 làm tiệm cận ngang.

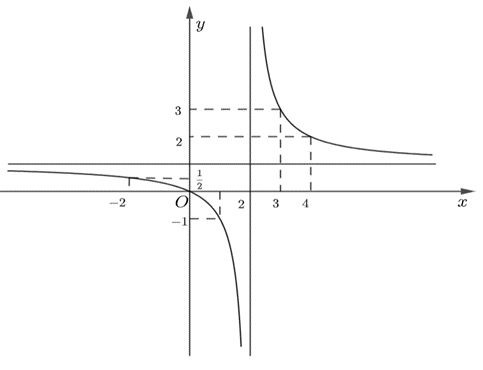
Đồ thị hàm số đi qua các điểm: (0; 0); $(- 2; \frac{1}{2})$ ; (1; – 1) (3; 3); (4; 2).

Ta có đồ thị hàm số như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Đồ thị nhận giao điểm của hai đường tiệm cận có tọa độ (2; 1) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

c) y = $\frac{x^{2} - 2 x + 2}{- x + 1}$

1) Tập xác định: D = ℝ\{1}.

2) Sự biến thiên.

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.

Ta có: $\lim_{x \to + \infty}$ y = −∞, $\lim_{x \to - \infty}$ y = +∞.

$\lim_{x \to 1^{-}}$ y = +∞, $\lim_{x \to 1^{+}}$ y = −∞.

Do đó, đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to + \infty}$ $\frac{y}{x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} - 2 x + 2}{(- x + 1) x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} - 2 x + 2}{- x^{2} + x}$ = −1.

$\lim_{x \to + \infty}$ [y – (−x)] = $\lim_{x \to + \infty}$ $(\frac{x^{2} - 2 x + 2}{- x + 1} + x)$ = $\lim_{x \to + \infty}$ $\frac{- x + 2}{- x + 1}$ = 1.

Do đó, đường thẳng y = −x + 1 là tiệm cận xiên của đồ thị hàm số.

Ta có: y' = $\frac{- x^{2} + 2 x}{{(- x + 1)}^{2}}$

y' = 0 ⇔ $\frac{- x^{2} + 2 x}{{(- x + 1)}^{2}}$ = 0 ⇔ x = 0 hoặc x = 2.

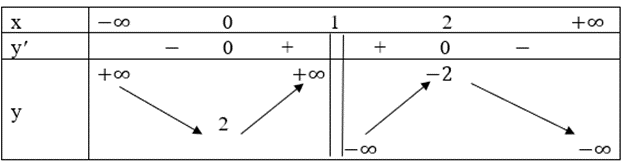
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Hàm số nghịch biến trên các khoảng (−∞; 0) và (2; +∞).

Hàm số đồng biến trên các khoảng (0; 1) và (1; 2).

Hàm số đạt cực tiểu tại x = 0, y_CT = 2; hàm số đạt cực đại tại x = 2, y_CĐ = −2.

3) Đồ thị

Đồ thị hàm số nhận đường thẳng x = 1 làm tiệm cận đứng và y = −x + 1 làm tiệm cận xiên.

Giao của đồ thị hàm số với trục tung là (0; 2).

Hàm số đi qua các điểm: $(- 2; \frac{10}{3})$ ; $(- 1; \frac{5}{2})$ ; (0; 2); (2; −2); $(3; \frac{- 5}{2})$ .

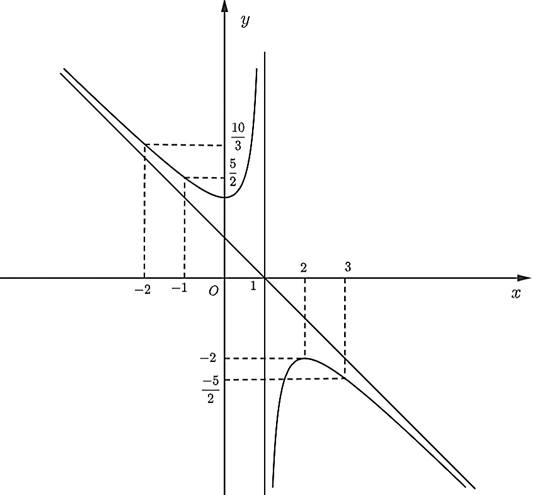
Ta có đồ thị hàm số:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (1; 0) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

d) y = $\frac{x^{2} + 2 x - 3}{x + 2}$

1) Tập xác định: D = ℝ\{−2}.

2) Sự biến thiên.

Giới hạn tại vô cực, giới hạn vô cực và các đường tiệm cận.

Ta có: $\lim_{x \to + \infty}$ y = +∞, $\lim_{x \to - \infty}$ y = −∞.

$\lim_{x \to - 2^{-}}$ y = +∞, $\lim_{x \to - 2^{+}}$ y = −∞.

Do đó, đường thẳng x = – 2 là tiệm cận đứng của đồ thị hàm số.

$\lim_{x \to + \infty}$ $\frac{y}{x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} + 2 x - 3}{(x + 2) x}$ = $\lim_{x \to + \infty}$ $\frac{x^{2} + 2 x - 3}{x^{2} + 2 x}$ = 1.

$\lim_{x \to + \infty}$ (y – x) = $\lim_{x \to + \infty}$ $(\frac{x^{2} + 2 x - 3}{x + 2} - x)$ = $\lim_{x \to + \infty}$ $\frac{- 3}{x + 2}$ = 0.

Do đó, đường thẳng y = x là tiệm cận xiên của đồ thị hàm số.

Ta có: y' = $\frac{x^{2} + 4 x + 7}{{(x + 2)}^{2}}$ = $1 + \frac{3}{{(x + 2)}^{2}}$ > 0, với ∀x ∈ D.

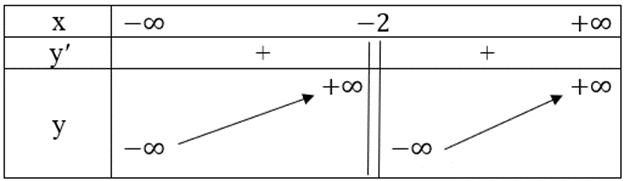
Ta có bảng biến thiên như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Hàm số đồng biến trên các khoảng (−∞; −2) và (−2; +∞).

3) Đồ thị

Đồ thị hàm số nhận đường thẳng x = − 2 làm tiệm cận đứng và y = x làm tiệm cận xiên.

Giao của đồ thị với trục tung tại điểm $(0; \frac{- 3}{2})$ ; giao của đồ thị với trục hoành tại các điểm (1; 0); (−3; 0).

Đồ thị hàm số đi qua các điểm: $(0; \frac{- 3}{2})$ ; (1; 0); (−3; 0); (−1; −4); (−5; −4); $(- 4; - \frac{5}{2}) .$

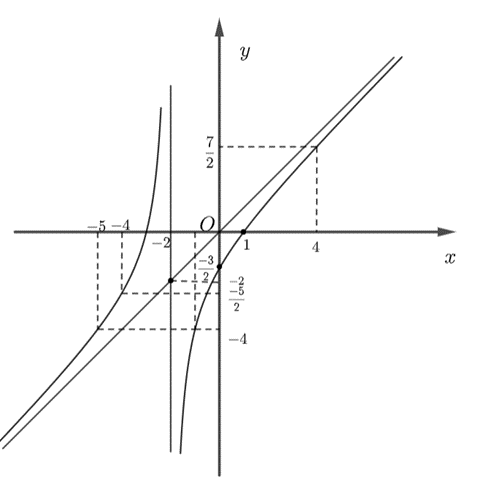
Ta có đồ thị như sau:

Khảo sát sự biến thiên và vẽ đồ thị của mỗi hàm số sau y = (2x-1)/(x+1)

Đồ thị hàm số nhận giao điểm của hai đường tiệm cận có tọa độ (−2; −2) làm tâm đối xứng và nhận phân giác của các góc tạo bởi hai đường tiệm cận đó làm trục đối xứng.

Lời giải SBT Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác:

Xem thêm các bài giải sách bài tập Toán lớp 12 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯