Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax^2 (a ≠ 0) đi qua điểm M(2; –2)

Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax (a ≠ 0) đi qua điểm M(2; –2).

Giải sách bài tập Toán 9 Bài tập cuối chương 6 - Chân trời sáng tạo

Bài 13 trang 18 sách bài tập Toán 9 Tập 2: Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax² (a ≠ 0) đi qua điểm M(2; –2).

a) Tìm hệ số a, vẽ (P) với a vừa tìm được.

b) Tìm tung độ của điểm thuộc parabol có hoành độ x = –3.

c) Tìm các điểm thuộc parabol có tung độ y = –4,5.

Lời giải:

a) Đồ thị hàm số (P): y = ax² đi qua điểm M(2; –2) nên thay x = 2; y = –2 vào hàm số y = ax², ta được

‒2 = a.2² hay 4a = ‒2, suy ra $a = - \frac{1}{2} .$

Vậy $(P) : y = - \frac{1}{2} x^{2} .$

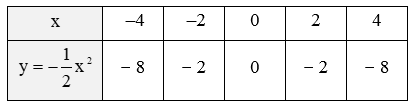
Ta có bảng giá trị của hàm số:

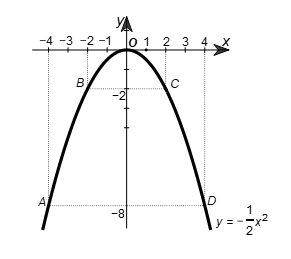
Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax^2 (a ≠ 0) đi qua điểm M(2; –2)

• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(‒4; ‒8); B (‒2; ‒2); O(0; 0); C(2; ‒2); D(4; ‒8).

• Đồ thị của hàm số $y = - \frac{x^{2}}{2}$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.

Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax^2 (a ≠ 0) đi qua điểm M(2; –2)

b) Thay x = –3 vào hàm số $y = - \frac{1}{2} x^{2},$ ta được $y = - \frac{1}{2} \cdot {(- 3)}^{2} = - \frac{9}{2} .$

Vậy tung độ của điểm thuộc parabol có hoành độ x = –3 là bằng $- \frac{9}{2} .$

c) Thay y = –4,5 vào hàm số $y = - \frac{1}{2} x^{2},$ ta được:

$- 4, 5 = - \frac{1}{2} x^{2},$ suy ra x² = 9, do đó x = 3; x = –3.

Vậy các điểm (–3; –4,5) và (3; –4,5) thuộc parabol có tung độ y = –4,5.

Lời giải SBT Toán 9 Bài tập cuối chương 6 hay khác: