Vẽ đồ thị (P) của hàm số y = (2/3) x^2 và đường thẳng d: y = (-1/3)x + 1 trên cùng một mặt phẳng toạ độ Oxy

---

a) Vẽ đồ thị (P) của hàm số và đường thẳng trên cùng một mặt phẳng toạ độ Oxy.

Giải sách bài tập Toán 9 Bài tập cuối chương 6 - Chân trời sáng tạo

Bài 14 trang 18 sách bài tập Toán 9 Tập 2: a) Vẽ đồ thị (P) của hàm số $y=\frac{2}{3}{x}^2$ và đường thẳng $d:y=-\frac{1}{3}x+1$ trên cùng một mặt phẳng toạ độ Oxy.

b) Tìm tọa độ giao điểm của (P) và d bằng phép tính.

Lời giải:

a) ‒ Vẽ đồ thị hàm số $y=\frac{2}{3}{x}^2$

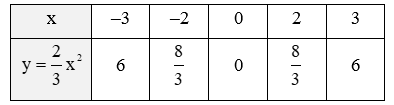
Ta có bảng giá trị của hàm số:

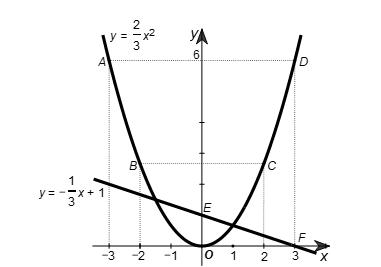
• Trên mặt phẳng tọa độ Oxy, lấy các điểm A(–3; 6); $B\left(-2;\frac{8}{3}\right);$ O(0; 0); $C\left(2;\frac{8}{3}\right);$ D(3; 6).

• Đồ thị của hàm số $y=\frac{2}{3}{x}^2$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như hình vẽ.

‒ Vẽ đường thẳng $d:y=-\frac{1}{3}x+1$

⦁ Cho x = 0 ta có y = 1. Đường thẳng d đi qua điểm E(0; 1).

⦁ Cho x = 3 ta có y = 0. Đường thẳng d đi qua điểm F(3; 0).

Đồ thị hàm số $y=-\frac{1}{3}x+1$ là đường thẳng d đi qua hai điểm E(0; 1) và F(3; 0).

Đồ thị (P) của hàm số $y=\frac{2}{3}{x}^2$ và đường thẳng $d:y=-\frac{1}{3}x+1$ được vẽ như sau:

b) Gọi (x₀; y₀) là tọa độ giao điểm của (P) và d.

Khi đó, ta có $y_0=\frac{2}{3}{x}_0^2$ và $y_0=-\frac{1}{3}{x}_0+1.$

Suy ra $\frac{2}{3}{x}_0^2=-\frac{1}{3}{x}_0+1$

           $\frac{2}{3}{x}_0^2+\frac{1}{3}{x}_0-1=0$

           $2x_0^2+x_0-3=0$

Phương trình trên a + b + c = 2 + 1 ‒ 3 = 0 nên phương trình có hai nghiệm phân biệt là $x_1=1;x_2=-\frac{3}{2}.$

Thay x₁ = 1 vào hàm số $y=\frac{2}{3}{x}^2,$ ta được $y_1=\frac{2}{3}\cdot 1^2=\frac{2}{3}.$

Thay $x_2=-\frac{3}{2}$ vào hàm số $y=\frac{2}{3}{x}^2,$ ta được $y_2=\frac{2}{3}\cdot {\left(-\frac{3}{2}\right)}^2=\frac{2}{3}\cdot \frac{9}{4}=\frac{3}{2}.$

Vậy toạ độ giao điểm của (P) và d là $\left(1;\frac{2}{3}\right)$ và $\left(-\frac{3}{2};\frac{3}{2}\right).$

Lời giải SBT Toán 9 Bài tập cuối chương 6 hay khác:

• Câu 1 trang 16 sách bài tập Toán 9 Tập 2: Điểm nào sau đây thuộc đồ thị của hàm số $y=-\frac{2}{3}{x}^2?$...

• Câu 2 trang 16 sách bài tập Toán 9 Tập 2: Cho hàm số y = x². Khi y = 4 thì...

• Câu 3 trang 16 sách bài tập Toán 9 Tập 2: Đồ thị của hàm số y = ax² (a ≠ 0) đi qua điểm A(1; – 2). Giá trị của a bằng...

• Câu 4 trang 16 sách bài tập Toán 9 Tập 2: Cho phương trình ax² + bx + c = 0 (a ≠ 0) có ∆ = b² – 4ac = 0. Khi đó, phương trình có hai nghiệm là:...

• Câu 5 trang 16 sách bài tập Toán 9 Tập 2: Nghiệm của phương trình x² – 15x – 16 = 0 là...

• Câu 6 trang 16 sách bài tập Toán 9 Tập 2: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?...

• Câu 7 trang 16 sách bài tập Toán 9 Tập 2: Gọi S và P lần lượt là tổng và tích hai nghiệm của phương trình x² + 3x – 70 = 0. Khi đó, giá trị của S và P là...

• Câu 8 trang 16 sách bài tập Toán 9 Tập 2: Cho phương trình x² + 6x – 91 = 0. Gọi x>₁, x₂ là hai nghiệm của phương trình...

• Câu 9 trang 17 sách bài tập Toán 9 Tập 2: Cho hàm số y = ax² Giá trị a để đồ thị của hàm số đi qua điểm (2; 2) là a = 2(a ≠ 0)....

• Câu 10 trang 17 sách bài tập Toán 9 Tập 2: Cho phương trình 5x² – 7x + 2 = 0. Phương trình có a – b + c = 0 nên có hai nghiệm là $x_1=-1;x_2=-\frac{c}{a}=-\frac{2}{5}.$...

• Câu 11 trang 17 sách bài tập Toán 9 Tập 2: Cho phương trình ax² + bx + c = 0 (a ≠ 0). Khi ∆ = 0, phương trình có nghiệm kép $x_1=x_2=-\frac{b}{a}.$...

• Bài 12 trang 17 sách bài tập Toán 9 Tập 2: Cho hai hàm số $y=\frac{3}{4}{x}^2$ và $y=-\frac{3}{4}{x}^2.$ Vẽ đồ thị của hai hàm số trên cùng một mặt phẳng tọa độ..

• Bài 13 trang 18 sách bài tập Toán 9 Tập 2: Trên mặt phẳng toa độ Oxy, cho parabol (P): y = ax² (a ≠ 0) đi qua điểm M(2; –2)....

• Bài 15 trang 18 sách bài tập Toán 9 Tập 2: Giải các phương trình: $7x^2+14\sqrt{5}x=0;$...

• Bài 16 trang 18 sách bài tập Toán 9 Tập 2: Giải các phương trình: 3x² + 23x – 36 = 0...

• Bài 17 trang 18 sách bài tập Toán 9 Tập 2: Giải các phương trình: $x^2-\left(3+\sqrt{5}\right)x+3\sqrt{5}=0;$...

• Bài 18 trang 18 sách bài tập Toán 9 Tập 2: Tìm hai số u và v (nếu có) trong mỗi trường hợp sau: u + v = –2, uv = –35...

• Bài 19 trang 18 sách bài tập Toán 9 Tập 2: Cho phương trình 2x² – 9x – 5 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của các biểu thức sau:...

• Bài 20 trang 18 sách bài tập Toán 9 Tập 2: Cho phương trình 5x² – 7x + 1 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Không giải phương trình, hãy tính giá trị của biểu thức...

• Bài 21 trang 18 sách bài tập Toán 9 Tập 2: Một công nhân theo kế hoạch phải làm 120 sản phẩm trong một thời gian nhất định. Do cải tiến kĩ thuật nên thực tế mỗi ngày người đó đã làm được nhiều hơn 3 sản phẩm ...

• Bài 22 trang 19 sách bài tập Toán 9 Tập 2: Một mảnh vườn hình chữ nhật có diện tích 1 000 m². Nếu tăng chiều dài thêm 10 m, giảm chiều rộng đi 5 m thì diện tích mảnh vườn không thay đổi...

• Bài 23 trang 19 sách bài tập Toán 9 Tập 2: Một ô tô dự định đi từ tỉnh A đến tỉnh B cách nhau 180 km trong một thời gian nhất định. Sau khi đi được 1 giờ, ô tô bị hỏng nên phải dừng lại 20 phút để sửa...

• Bài 24 trang 19 sách bài tập Toán 9 Tập 2: Một phòng họp có 420 cái ghế được chia thành các dãy có số ghế bằng nhau. Nếu thêm cho mỗi dãy 7 cái ghế ...

• Bài 25 trang 19 sách bài tập Toán 9 Tập 2: Người ta trộn 8 g chất lỏng A với 6 g chất lỏng B để được hỗn hợp có khối lượng riêng là 0,7 g/cm³....