Bài 2 trang 77 Toán 10 Tập 1 Cánh diều

Cho tam giác ABC có AB = 5, BC = 7,. Tính độ dài cạnh AC.

Giải Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Bài 2 trang 77 Toán lớp 10 Tập 1: Cho tam giác ABC có AB = 5, BC = 7, $\hat{A} = 120 °$ . Tính độ dài cạnh AC.

Lời giải:

Cách 1: áp dụng định lí sin và côsin

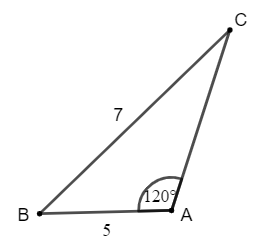
Bài 2 trang 77 Toán 10 Tập 1 Cánh diều

Áp dụng định lí sin trong tam giác ABC ta có: $\frac{A B}{\sin C} = \frac{B C}{\sin A}$

$\Rightarrow \sin C = \frac{A B . \sin A}{B C} = \frac{5. \sin 120 °}{7} = \frac{5 \sqrt{3}}{14}$ .

Do đó: $\hat{C} \approx 38,2 °$ .

Lại có $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{B} = 180 ° - (\hat{A} + \hat{C}) = 180 ° - (120 ° + 38,2 °) = 21,8 °$ .

Áp dụng định lí côsin trong tam giác ABC ta có:

AC² = AB² + BC² – 2 . AB . AC . cos B = 5² + 7² – 2 . 5 . 7 . cos 21,8° ≈ 9

⇒ AC ≈ 3.

Cách 2: Dựng thêm đường cao và sử dụng định lí Pythagore.

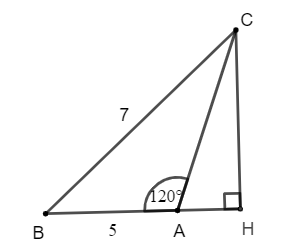
Bài 2 trang 77 Toán 10 Tập 1 Cánh diều

Dựng đường cao CH của tam giác ABC.

Đặt AH = x.

Ta có: $\hat{B A C} + \hat{C A H} = 180 °$ ( kề bù).

$\Rightarrow \hat{C A H} = 180 ° - \hat{B A C} = 180 ° - 120 ° = 60 °$ .

Tam giác ACH vuông tại H nên

$c o s \hat{C A H} = \frac{A H}{C A} \Rightarrow C A = \frac{A H}{c o s \hat{C A H}} = \frac{x}{c o s 60 °} = \frac{x}{\frac{1}{2}} = 2 x$ .

Áp dụng định lí Pythagore ta tính được: $C H = x \sqrt{3}$ .

Và BC² = BH²+ CH² = (BA + AH)² + CH²

Thay số: 7²= (5 + x)² + 3x² (1)

Giải phương trình (1) ta được x = 1,5 là giá trị thỏa mãn.

Suy ra AC = 2x = 2 . 1,5 = 3.

Lời giải bài tập Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác hay, chi tiết khác: