Hoạt động 5 trang 75 Toán 10 Tập 1 Cánh diều

❮ Bài trước Bài sau ❯

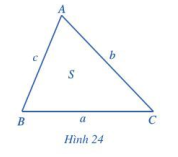
Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).

Giải Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Hoạt động 5 trang 75 Toán lớp 10 Tập 1: Cho tam giác ABC có BC = a, CA = b, AB = c và diện tích S (Hình 24).

a) Từ định lí côsin, chứng tỏ rằng:

$\sin A = \frac{2}{b c} \sqrt{p (p - a) (p - b) (p - c)}$ , ở đó $p = \frac{a + b + c}{2}$ .

b) Bằng cách sử dụng công thức $S = \frac{1}{2} b c \sin A$ , hãy chứng tỏ rằng:

$S = \sqrt{p (p - a) (p - b) (p - c)}$ .

Lời giải:

a) Áp dụng định lí côsin trong tam giác ABC ta có:

BC² = AB² + AC² – 2 . AB . AC . cos A

$\Rightarrow \cos A = \frac{A B^{2} + A C^{2} - B C^{2}}{2. A B . A C} = \frac{b^{2} + c^{2} - a^{2}}{2 b c}$ (1)

Ta lại có: sin² A + cos² A = 1

Do đó: sin² A = 1 – cos² A

Vì góc A là một góc của tam giác ABC nên 0° < $\hat{A}$ < 180° nên sin A > 0.

Nên $\sin A = \sqrt{1 - \cos^{2} A}$ (2)

Từ (1) và (2) ta có:

$\sin A = \sqrt{1 - \cos^{2} A}$ $= \sqrt{\frac{{(2 b c)}^{2}}{{(2 b c)}^{2}} - \frac{{(b^{2} + c^{2} - a^{2})}^{2}}{{(2 b c)}^{2}}}$

$= \sqrt{\frac{{(2 b c)}^{2} - {(b^{2} + c^{2} - a^{2})}^{2}}{{(2 b c)}^{2}}}$ $= \sqrt{\frac{(2 b c + b^{2} + c^{2} - a^{2}) (2 b c - b^{2} - c^{2} + a^{2})}{{(2 b c)}^{2}}}$

$= \frac{\sqrt{({(b + c)}^{2} - a^{2}) (a^{2} - {(b - c)}^{2})}}{2 b c}$ $= \frac{\sqrt{(b + c + a) (b + c - a) (a + b - c) (a - b + c)}}{2 b c}$

$= \frac{\sqrt{(a + b + c) (a + b + c - 2 a) (a + b + c - 2 c) (a + b + c - 2 b)}}{2 b c}$

Lại có $p = \frac{a + b + c}{2} \Rightarrow a + b + c = 2 p$

Khi đó: $\sin A = \frac{\sqrt{2 p . (2 p - 2 a) (2 p - 2 b) (2 p - 2 c)}}{2 b c}$ $= \frac{\sqrt{16 p (p - a) (p - b) (p - c)}}{2 b c}$

Vậy $\sin A = \frac{2}{b c} \sqrt{p (p - a) (p - b) (p - c)}$ .

b) Diện tích tam giác ABC là $S = \frac{1}{2} b c \sin A$ .

Mà $\sin A = \frac{2}{b c} \sqrt{p (p - a) (p - b) (p - c)}$

Nên $S = \frac{1}{2} b c . \frac{2}{b c} \sqrt{p (p - a) (p - b) (p - c)} = \sqrt{p (p - a) (p - b) (p - c)}$ .

Vậy $S = \sqrt{p (p - a) (p - b) (p - c)}$ .

Lời giải bài tập Toán 10 Bài 2: Giải tam giác. Tính diện tích tam giác hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 10 Cánh diều

Hoạt động 5 trang 75 Toán 10 Tập 1 Cánh diều

Giải Toán lớp 10 Bài 2: Giải tam giác. Tính diện tích tam giác

Xem thêm lời giải bài tập Toán lớp 10 Cánh diều hay, chi tiết khác: