Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và
Câu hỏi:
Tam giác ABC vuông tại A có AB = AC = 30 cm. Hai đường trung tuyến BE và CF cắt nhau tại G. Diện tích tam giác GEC là:
A. cm2;
B. 50 cm2;
C. 75 cm2;
D. cm2.
Trả lời:
Hướng dẫn giải
Đáp án đúng là: C
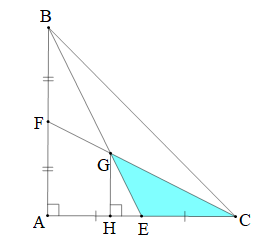
Vì BE là trung tuyến của tam giác ABC nên E là trung điểm của AC.
Do đó
Hai đường trung tuyến BE và CF cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Khi đó (tính chất trọng tâm của tam giác)
Hay
Gọi H là chân đường vuông góc kẻ từ G xuống AC.
Suy ra GH // AB.
Do đó (định lí Ta – let trong tam giác ABE)
Hay
Diện tích tam giác GEC là:
Vậy diện tích tam giác GEC là 75 cm2.
Xem thêm bài tập trắc nghiệm Toán 10 CTST có lời giải hay khác:
Câu 1:
Tam giác ABC có . Số đo góc là:
Xem lời giải »
Câu 2:
Tam giác ABC có , AC = 10. Độ dài cạnh AB là:
Xem lời giải »
Câu 3:
Tam giác ABC có AB = 3, BC = 6. Số đo góc B là:
Xem lời giải »
Câu 4:
Cho tam giác ABC nội tiếp đường tròn bán kính R, AB = R, Tính số đo của biết là góc tù.
Xem lời giải »
Câu 5:
Bán kính đường tròn nội tiếp tam giác có ba cạnh lần lượt là 5, 12, 13 là:
Xem lời giải »
Câu 6:
Tam giác ABC có BC = a, CA = b, AB = c và có diện tích S. Nếu tăng cạnh BC lên 2 lần đồng thời tăng cạnh AC lên 3 lần và giữ nguyên độ lớn của góc C thì khi đó diện tích của tam giác mới được tạo nên bằng:
Xem lời giải »
Câu 7:
Hình bình hành có một cạnh là 4, hai đường chéo là 6 và 8. Độ dài cạnh kề với cạnh có độ dài bằng 4 là:
Xem lời giải »
Câu 8:
Tam giác ABC vuông cân tại A và nội tiếp trong đường tròn tâm O, bán kính R. Gọi r là bán kính đường tròn nội tiếp tam giác ABC. Tỉ số là:
Xem lời giải »


