Luyện tập 1 trang 56 Toán 10 Tập 1 - Kết nối tri thức

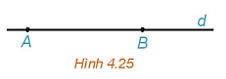
Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?

Giải Toán lớp 10 Bài 9: Tích của một vectơ với một số

Luyện tập 1 trang 56 Toán 10 Tập 1: Cho đường thẳng d đi qua hai điểm phân biệt A và B (H.4.25). Những khẳng định nào sau đây là đúng?

a) Điểm M thuộc đường thẳng d khi và chỉ khi tồn tại số t để $\vec{A M} = t \vec{A B}$ .

b) Với điểm M bất kì, ta luôn có: $\vec{A M} = \frac{A M}{A B} . \vec{A B} .$

c) Điểm M thuộc tia đối của tia AB khi và chỉ khi tồn tại số t ≤ 0 để $\vec{A M} = t \vec{A B} .$

Luyện tập 1 trang 56 Toán 10 Tập 1 | Kết nối tri thức Giải Toán lớp 10

Lời giải:

a) Nếu M thuộc đường thẳng d thì $\vec{A M}$ cùng phương $\vec{A B}$

Do đó ta có tồn tại một số thực t thỏa mãn $\vec{A M} = t \vec{A B} .$

Nếu tồn tại số t thỏa mãn $\vec{A M} = t \vec{A B}$ thì $\vec{A M}$ cùng phương $\vec{A B}$ hay $\vec{A M}$ trùng với $\vec{A B}$ .

Do đó A, M, B thẳng hàng hay M thuộc đường thẳng d.

Vì thế khẳng định a) đúng.

b) Nếu M không thuộc đường thẳng d thì $\vec{A M}$ và $\vec{A B}$ không cùng phương. Do đó $\vec{A M} \neq \frac{A M}{A B} \vec{A B} .$

Vì vậy khẳng định b) sai.

c) Nếu điểm M thuộc tia đối của tia AB:

Luyện tập 1 trang 56 Toán 10 Tập 1 | Kết nối tri thức Giải Toán lớp 10

Thì ta có: $\vec{M A} = t \vec{M B}$ với t < 0.

Do đó khẳng định c) sai.

Lời giải bài tập Toán 10 Bài 9: Tích của một vectơ với một số hay, chi tiết khác:

<<<<<<< HEAD ======= >>>>>>> 7de0ce75c76253c52280308e94cf2d713ccea5e2