Hoạt động 1 trang 59 Toán 11 Tập 1 Cánh diều

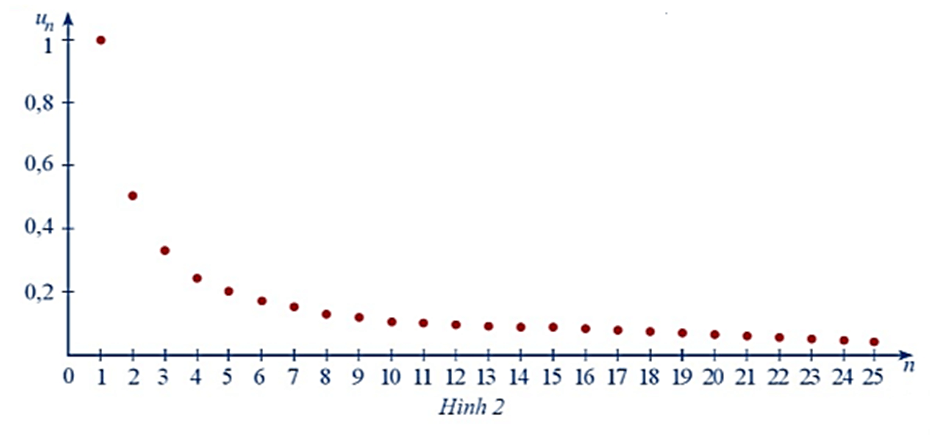
Hình 2 biểu diễn các số hạng của dãy số (u), với u­ = trên hệ trục tọa độ.

Giải Toán 11 Bài 1: Giới hạn của dãy số - Cánh diều

Hoạt động 1 trang 59 Toán 11 Tập 1: Hình 2 biểu diễn các số hạng của dãy số (u_n), với u­_n = $\frac{1}{n}$trên hệ trục tọa độ.

a) Nhận xét về sự thay đổi các giá trị u_n khi n ngày càng lớn.

b) Hoàn thành bảng và trả lời câu hỏi sau:

Kể từ số hạng u_n nào của dãy số thì khoảng cách từ u_n đến 0 nhỏ hơn 0,001? 0,0001?

Lời giải:

a) Khi n ngày càng lớn thì giá trị của u_n càng giảm dần về 0.

b) Ta có bảng:

Kể từ số hạng u₁₀₀₁ trở đi thì khoảng cách từ u_n đến 0 nhỏ hơn 0,001.

Kể từ số hạng u_{10 001} trở đi thì khoảng cách từ u_n đến 0 nhỏ hơn 0,0001.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số hay, chi tiết khác:

• Câu hỏi khởi động trang 59 Toán 11 Tập 1: Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ....

• Luyện tập 1 trang 60 Toán 11 Tập 1: Chứng minh rằng: a) lim 0 = 0 ....

• Hoạt động 2 trang 60 Toán 11 Tập 1: Cho dãy số (u_n), với u_n = 2 + $\frac{1}{n}$ ....

• Luyện tập 2 trang 61 Toán 11 Tập 1: Chứng minh rằng: lim$\frac{-4n+1}{n}$=-4 ....

• Luyện tập 3 trang 62 Toán 11 Tập 1: Chứng minh rằng: lim${\left(\frac{e}{\pi }\right)}^n$ = 0 ....

• Hoạt động 3 trang 62 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 8+$\frac{1}{n}$ ....

• Luyện tập 4 trang 62 Toán 11 Tập 1: Tính các giới hạn sau: a) lim$\frac{8n^2+n}{n^2}$ ....

• Hoạt động 4 trang 63 Toán 11 Tập 1: Cho cấp số nhân (u_n), với u₁ = 1 và công bội q=$\frac{1}{2}$ ....

• Luyện tập 5 trang 63 Toán 11 Tập 1: Tính tổng M = 1-$\frac{1}{2}+\frac{1}{2^2}-\mathrm{...}+{\left(-\frac{1}{2}\right)}^{n-1}+\mathrm{...}$ ....

• Luyện tập 6 trang 63 Toán 11 Tập 1: Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng ....

• Hoạt động 5 trang 63 Toán 11 Tập 1: Quan sát dãy số (u_n) với u­_n = n² và cho biết giá trị của n_n có thể lớn hơn ....

• Luyện tập 7 trang 64 Toán 11 Tập 1: Tính lim(– n³) ....

• Luyện tập 8 trang 64 Toán 11 Tập 1: Chứng tỏ rằng lim$\frac{n-1}{n^2}$=0 ....

• Bài 1 trang 64 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 3 + $\frac{1}{n}$, v_n = 5 –$\frac{2}{n^2}$ ....

• Bài 2 trang 65 Toán 11 Tập 1: Tính các giới hạn sau: a) lim$\frac{5n+1}{2n}$ ....

• Bài 3 trang 65 Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (u_n­), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$ ....

• Bài 4 trang 65 Toán 11 Tập 1: Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông ....

• Bài 5 trang 65 Toán 11 Tập 1: Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm ....

• Bài 6 trang 65 Toán 11 Tập 1: Gọi C là nửa đường tròn đường kính AB = 2R ....