Câu hỏi khởi động trang 59 Toán 11 Tập 1 Cánh diều

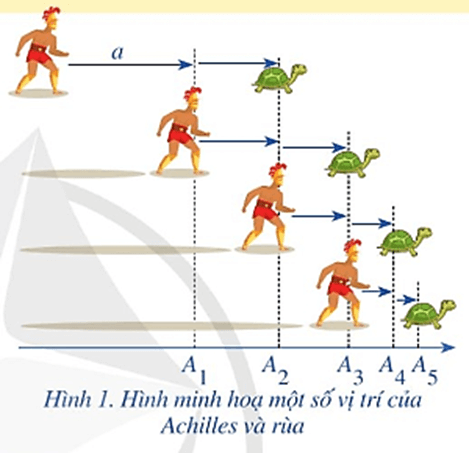
Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1). Quá trình này tiếp tục vô hạn. Vì thế, Achilles không bao giờ đuổi kịp rùa.

Giải Toán 11 Bài 1: Giới hạn của dãy số - Cánh diều

Câu hỏi khởi động trang 59 Toán 11 Tập 1: Zénon (Zê – nông, 496 – 429 trước Công Nguyên) là một triết gia Hy Lạp ở thành phố Edée đã phát biểu nghịch lí như sau: Achilles (A – sin) là một lực sĩ trong thần thoại Hy Lạp, người được mệnh danh là “có đôi chân chạy nhanh như gió” đuổi theo một con rùa trên một đường thẳng. Nếu lúc xuất phát, rùa ở điểm A₁ cách Achilles một khoảng bằng a khác 0. Khi Achilles chạy đến vị trí của rùa xuất phát thì rùa chạy về phía trước một khoảng (như Hình 1). Quá trình này tiếp tục vô hạn. Vì thế, Achilles không bao giờ đuổi kịp rùa.

Trên thực tế, Achilles không đuổi kịp rùa là vô lí. Kiến thức toán học nào có thể giải thích được nghịch lí Zénon nói trên là không đúng?

Lời giải:

Giới hạn hữu hạn của hàm số có thể giải thích được nghịch lí Zénon nói trên là không đúng. Trong bài học ngày hôm nay chúng ta sẽ tìm hiểu về điều đó.

Lời giải bài tập Toán 11 Bài 1: Giới hạn của dãy số hay, chi tiết khác:

• Hoạt động 1 trang 59 Toán 11 Tập 1: Hình 2 biểu diễn các số hạng của dãy số (u_n), với u­_n = $\frac{1}{n}$ ....

• Luyện tập 1 trang 60 Toán 11 Tập 1: Chứng minh rằng: a) lim 0 = 0 ....

• Hoạt động 2 trang 60 Toán 11 Tập 1: Cho dãy số (u_n), với u_n = 2 + $\frac{1}{n}$ ....

• Luyện tập 2 trang 61 Toán 11 Tập 1: Chứng minh rằng: lim$\frac{-4n+1}{n}$=-4 ....

• Luyện tập 3 trang 62 Toán 11 Tập 1: Chứng minh rằng: lim${\left(\frac{e}{\pi }\right)}^n$ = 0 ....

• Hoạt động 3 trang 62 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 8+$\frac{1}{n}$ ....

• Luyện tập 4 trang 62 Toán 11 Tập 1: Tính các giới hạn sau: a) lim$\frac{8n^2+n}{n^2}$ ....

• Hoạt động 4 trang 63 Toán 11 Tập 1: Cho cấp số nhân (u_n), với u₁ = 1 và công bội q=$\frac{1}{2}$ ....

• Luyện tập 5 trang 63 Toán 11 Tập 1: Tính tổng M = 1-$\frac{1}{2}+\frac{1}{2^2}-\mathrm{...}+{\left(-\frac{1}{2}\right)}^{n-1}+\mathrm{...}$ ....

• Luyện tập 6 trang 63 Toán 11 Tập 1: Giải thích vì sao nghịch lí Zénon trong phần mở đầu là không đúng ....

• Hoạt động 5 trang 63 Toán 11 Tập 1: Quan sát dãy số (u_n) với u­_n = n² và cho biết giá trị của n_n có thể lớn hơn ....

• Luyện tập 7 trang 64 Toán 11 Tập 1: Tính lim(– n³) ....

• Luyện tập 8 trang 64 Toán 11 Tập 1: Chứng tỏ rằng lim$\frac{n-1}{n^2}$=0 ....

• Bài 1 trang 64 Toán 11 Tập 1: Cho hai dãy số (u_n), (v_n) với u_n = 3 + $\frac{1}{n}$, v_n = 5 –$\frac{2}{n^2}$ ....

• Bài 2 trang 65 Toán 11 Tập 1: Tính các giới hạn sau: a) lim$\frac{5n+1}{2n}$ ....

• Bài 3 trang 65 Toán 11 Tập 1: a) Tính tổng của cấp số nhân lùi vô hạn (u_n­), với u₁=$\frac{2}{3}$, q=-$\frac{1}{4}$ ....

• Bài 4 trang 65 Toán 11 Tập 1: Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông ....

• Bài 5 trang 65 Toán 11 Tập 1: Có 1 kg chất phóng xạ độc hại. Biết rằng, cứ sau một khoảng thời gian T = 24 000 năm ....

• Bài 6 trang 65 Toán 11 Tập 1: Gọi C là nửa đường tròn đường kính AB = 2R ....