Bài 6 trang 85 Toán 11 Tập 1 Chân trời sáng tạo

Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?

Giải Toán 11 Bài 3: Hàm số liên tục - Chân trời sáng tạo

Bài 6 trang 85 Toán 11 Tập 1: Lực hấp dẫn do Trái Đất tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm của nó là F(r) = 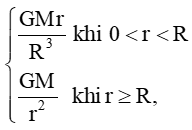trong đó M là khối lượng, R là bán kính của Trái Đất, G là hằng số hấp dẫn. Hàm số F(r) có liên tục trên (0; +∞) không?

Lời giải:

+) Ta có: y = $\frac{GMr}{R^3}$ liên tục trên (0; R) và y = $\frac{GM}{r^2}$ liên tục trên (R; + ∞).

+) Tại r = R, ta có:

$\underset{r\to R^{-}}{\lim }F\left(r\right)=\underset{r\to R^{-}}{\lim }\frac{GMr}{R^3}=\frac{GM}{R^2}$

$\underset{r\to R^{+}}{\lim }F\left(r\right)=\underset{r\to R^{-}}{\lim }\frac{GM}{r^2}=\frac{GM}{R^2}$

Suy ra $\underset{r\to R^{-}}{\lim }F\left(r\right)=\underset{r\to R^{+}}{\lim }F\left(r\right)$. Do đó $\underset{r\to R}{\lim }F\left(r\right)=\frac{GM}{R^2}$

Mà $F\left(R\right)=\frac{GM}{R^2}$ nên $\underset{r\to R}{\lim }F\left(r\right)=F\left(R\right)=\frac{GM}{R^2}$

Suy ra hàm số liên tục tại x = R.

Vậy hàm số liên tục trên (0; +∞).

Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:

• Hoạt động khởi động trang 80 Toán 11 Tập 1: Hai đồ thị ở hai hình dưới đây cho biết phí gửi xe y của ô tô con ....

• Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số có đồ thị như Hình 1 ....

• Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) f(x) = 1 – x² tại điểm x₀ = 3 ....

• Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số ....

• Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: $y=\sqrt{x-1}+\sqrt{2-x}$ trên [1; 2] ....

• Vận dụng 1 trang 82 Toán 11 Tập 1: Tại một xưởng sản xuất bột đá thạch anh, giá bán (tính theo nghìn đồng) của x (kg) bột đá thạch anh được tính theo công thức sau ....

• Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = $\frac{1}{x-1}$ ....

• Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số $y=\sqrt{x^2-4}$ ....

• Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = ....

• Vận dụng 2 trang 83 Toán 11 Tập 1: Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau ....

• Hoạt động khám phá 4 trang 83 Toán 11 Tập 1: Cho hai hàm số y = f(x) = $\frac{1}{x-1}$ ....

• Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) y = $\sqrt{x^2+1}$ + 3 - x ....

• Vận dụng 3 trang 84 Toán 11 Tập 1: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) tâm O, bán kính bằng 1 ....

• Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) = ....

• Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = ....

• Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) = $\frac{x}{x^2-4}$ ....

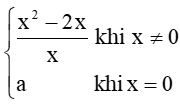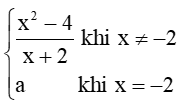• Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x) = $\sqrt{x-1}$ ....

• Bài 5 trang 85 Toán 11 Tập 1: Một bãi đậu xe ô tô đưa ra giá C(x) (đồng) khi thời gian đậu xe là x (giờ) như sau: ....