Vận dụng 2 trang 83 Toán 11 Tập 1 Chân trời sáng tạo
Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:
Giải Toán 11 Bài 3: Hàm số liên tục - Chân trời sáng tạo
Vận dụng 2 trang 83 Toán 11 Tập 1: Một hãng taxi đưa ra giá cước T(x) (đồng) khi đi quãng đường x (km) cho loại xe 4 chỗ như sau:
T(x) =
Xét tính liên tục của hàm số T(x).
Lời giải:
+) Với x0 ∈ (0; 0,7) hàm số f(x) = 10 000 là hàm đa thức nên liên tục trên (0; 0,7).
+) Với x0 ∈ (0,7; 20) hàm số f(x) = 10 000 + (x – 0,7).14 000 là hàm đa thức nên liên tục trên (0,7; 20).
+) Với x0 ∈ (20; +∞) hàm số f(x) = 280 200 + (x – 20).12 000 là hàm đa thức nên liên tục trên (20; +∞).
+) Tại x0 = 0,7 ta có:
;
[10 000 + (x-0,7).14 000] = 10 000.
Suy ra . Do đó tồn tại .
Mà f(0,7) = 10 000 nên = f(0,7) = 10000.
Vì vậy hàm số liên tục tại x0 = 0,7.
+) Tại x0 = 20 ta có:
[10 000 + (x-0,7).14 000] = 280 200.
[280 200+(x-20).12 000] = 280 200.
Suy ra . Do đó tồn tại .
Mà f(20) = 280 200 nên .
Vì vậy hàm số liên tục tại x = 20.
Vậy hàm số T(x) liên tục trên ℝ.
Lời giải bài tập Toán 11 Bài 3: Hàm số liên tục hay, chi tiết khác:
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số
có đồ thị như Hình 1 ....
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số
....
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: trên [1; 2] ....
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = ....
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số ....
Hoạt động khám phá 4 trang 83 Toán 11 Tập 1: Cho hai hàm số y = f(x) = ....
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số: a) y = + 3 - x ....
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) =
....
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau: a) f(x) = ....
Bài 4 trang 85 Toán 11 Tập 1: Cho hàm số f(x) = 2x – sinx, g(x) = ....



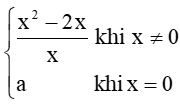 ....
....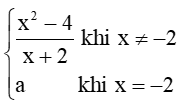 ....
....