Bài 7.13 trang 43 Toán 11 Tập 2 - Kết nối tri thức

❮ Bài trước Bài sau ❯

Giải Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng - Kết nối tri thức

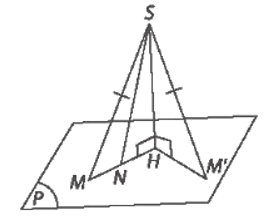
Bài 7.13 trang 43 Toán 11 Tập 2: Cho điểm S nằm ngoài mặt phẳng (P), có hình chiếu H trên (P). Với mỗi đểm M bất kì (không trùng H) trên mặt phẳng (P), ta gọi đoạn thẳng SM là đường xiên, đoạn thẳng HM là hình chiếu trên (P) của đường xiên đó. Chứng minh rằng:

a) Hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau;

b) Đường xiên SM lớn hơn đường xiên SM' nếu hình chiếu HM lớn hơn hình chiếu HM'.

Lời giải:

Bài 7.13 trang 43 Toán 11 Tập 2 | Kết nối tri thức Giải Toán 11

a) Có H là hình chiếu của S trên mặt phẳng (P) nên SH ⊥ (P), suy ra SH ⊥ HM, SH ⊥ HM'.

- Giả sử SM = SM'.

Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2

Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2.

Mà SM = SM' nên HM = HM'.

- Giả sử HM = HM'.

Xét tam giác SHM vuông tại H, có SM2 = SH2 + HM2

Xét tam giác SHM' vuông tại H, có SM'2 = SH2 + HM'2.

Mà HM = HM' nên SM = SM'.

Vậy hai đường xiên SM và SM' bằng nhau khi và chỉ khi hai hình chiếu HM và HM' tương ứng bằng nhau.

b) Trên tia HM lấy điểm N sao cho SN = SM' suy ra HN = HM'.

Mà SM > SM' nên SM > SN ⇒ HM > HN hay HM > HM'.

Lời giải bài tập Toán 11 Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 11 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved.