Hoạt động khởi động trang 6 Toán 12 Tập 1 Chân trời sáng tạo

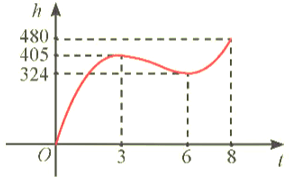
Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức h(t) = 6t – 81t + 324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào thì khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?

Giải Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số - Chân trời sáng tạo

Hoạt động khởi động trang 6 Toán 12 Tập 1: Trong 8 phút đầu kể từ khi xuất phát, độ cao h (tính bằng mét) của khinh khí cầu vào thời điểm t phút được cho bởi công thức h(t) = 6t³ – 81t² + 324t. Đồ thị của hàm số h(t) được biểu diễn trong hình bên. Trong các khoảng thời gian nào thì khinh khí cầu tăng dần độ cao, giảm dần độ cao? Độ cao của khinh khí cầu vào các thời điểm 3 phút và 6 phút sau khi xuất phát có gì đặc biệt?

Lời giải:

Dựa vào đồ thị ta thấy:

+) Trong khoảng thời gian từ 0 – 3 giây và 6 – 8 giây thì khinh khí cầu tăng dần độ cao.

+) Trong khoảng thời gian từ 3 – 6 giây thì khinh khí cầu giảm dần độ cao.

+) Tại thời điểm 3 phút sau khi xuất phát khinh khí cầu đang ở điểm chuyển từ tăng dần sang giảm dần nên độ cao của nó đang đạt cực đại.

+) Tại thời điểm 6 phút sau khi xuất phát, khinh khí cầu đang ở điểm chuyển từ giảm dần sang tăng dần nên độ cao của nó là một điểm cực tiểu.

Lời giải bài tập Toán 12 Bài 1: Tính đơn diệu và cực trị của hàm số hay, chi tiết khác:

• Thực hành 1 trang 7 Toán 12 Tập 1: Tìm các khoảng đơn điệu của hàm số y = f(x) có đồ thị cho ở Hình 3 ....

• Hoạt động khám phá 1 trang 7 Toán 12 Tập 1: Cho hàm số y = f(x) = x² ....

• Thực hành 2 trang 9 Toán 12 Tập 1: Xét tính đơn điệu của các hàm số sau ....

• Thực hành 3 trang 9 Toán 12 Tập 1: Chứng minh rằng hàm số f(x) = 3x – sinx đồng biến trên ℝ ....

• Vận dụng 1 trang 9 Toán 12 Tập 1: Hãy trả lời câu hỏi trong phần khởi động (trang 6) bằng cách xét dấu đạo hàm ....

• Hoạt động khám phá 2 trang 10 Toán 12 Tập 1: Quan sát đồ thị của hàm số y = f(x) = x³ – 3x² + 1 trong Hình 5 ....

• Thực hành 4 trang 11 Toán 12 Tập 1: Tìm các điểm cực trị của hàm số y = f(x) có đồ thị cho ở Hình 8 ....

• Hoạt động khám phá 3 trang 11 Toán 12 Tập 1: Đồ thị của hàm số $y=\left\{\begin{array}{l}{x}^2\text{ khi }x\le 1\\ 2-x\text{ khi }x>1\end{array}\right.$ được cho ở Hình 9 ....

• Thực hành 5 trang 12 Toán 12 Tập 1: Tìm cực trị của hàm số $g\left(x\right)=\frac{x^2+x+4}{x+1}$ ....

• Vận dụng 2 trang 12 Toán 12 Tập 1: Một phần lát cắt của dãy núi có độ cao tính bằng mét được mô tả bởi hàm số ....

• Bài 1 trang 13 Toán 12 Tập 1: Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11 ....

• Bài 2 trang 13 Toán 12 Tập 1: Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau ....

• Bài 3 trang 13 Toán 12 Tập 1: Tìm cực trị của các hàm số sau ....

• Bài 4 trang 13 Toán 12 Tập 1: Chứng minh rằng hàm số $y=\frac{2x+1}{x-3}$ nghịch biến trên từng khoảng xác định của nó ....

• Bài 5 trang 13 Toán 12 Tập 1: Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 và 2017 ....

• Bài 6 trang 13 Toán 12 Tập 1: Xét một chất điểm chuyển động dọc theo trục Ox ....

• Bài 7 trang 13 Toán 12 Tập 1: Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12 ....