Bài 1.4 trang 13 Toán 12 Tập 1 - Kết nối tri thức

Xét chiều biến thiên của các hàm số sau:

Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

Bài 1.4 trang 13 Toán 12 Tập 1: Xét chiều biến thiên của các hàm số sau:

a) $y = \sqrt{4 - x^{2}}$ ; b) $y = \frac{x}{x^{2} + 1}$ .

Lời giải:

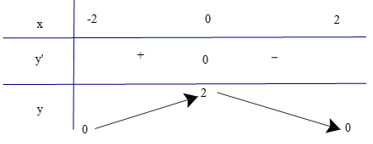
a) Tập xác định của hàm số là D = [−2; 2].

Có $y^{'} = \frac{{(4 - x^{2})}^{'}}{2 \sqrt{4 - x^{2}}} = \frac{- x}{\sqrt{4 - x^{2}}};$ y' = 0 ⇔ x = 0.

Lập bảng biến thiên của hàm số

Bài 1.4 trang 13 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Dựa vào bảng biến thiên, ta có

Hàm số đồng biến trên khoảng (−2; 0) và nghịch biến trên khoảng (0; 2).

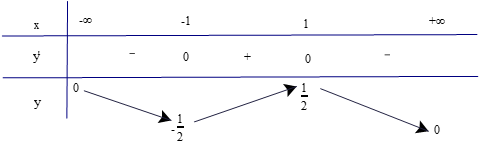
b) Tập xác định của hàm số là ℝ.

Có $y^{'} = \frac{(x^{2} + 1) - 2 x^{2}}{{(x^{2} + 1)}^{2}} = \frac{- x^{2} + 1}{{(x^{2} + 1)}^{2}}$ ; y' = 0 ⇔ −x² + 1 = 0 ⇔ x = 1 hoặc x = −1.

Lập bảng biến thiên của hàm số

Bài 1.4 trang 13 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Dựa vào bảng biến thiên, ta có:

Hàm số đồng biến trên khoảng (−1; 1).

Hàm số nghịch biến trên các khoảng (−∞; −1) và (1; +∞).

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác: