HĐ2 trang 7 Toán 12 Tập 1 - Kết nối tri thức

❮ Bài trước Bài sau ❯

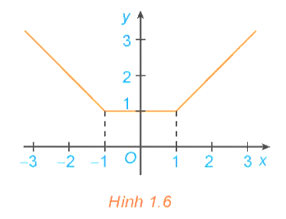
Xét hàm số có đồ thị như hình 1.6

Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số - Kết nối tri thức

HĐ2 trang 7 Toán 12 Tập 1: Xét hàm số y=−x  nê'u x<−11 nê'u −1≤x≤1x nê'u x>1 có đồ thị như hình 1.6

a) Xét dấu đạo hàm của hàm số trên các khoảng (−∞; −1), (1; +∞). Nêu nhận xét về mối quan hệ giữa tính đồng biến, nghịch biến và dấu đạo hàm của hàm số trên mỗi khoảng này.

b) Có nhận xét gì về đạo hàm y' và hàm số y trên khoảng (−1;1)?

HĐ2 trang 7 Toán 12 Tập 1 | Kết nối tri thức Giải Toán 12

Lời giải:

a) +) Với x < −1, ta có y' = −1 < 0.

+) Với x > 1, ta có y' = 1 > 0.

Nhận xét:

+ Với x ∈ (−∞; −1), ta có y' < 0 thì hàm số nghịch biến.

+ Với x ∈ (1; +∞), ta có y' > 0 thì hàm số đồng biến.

b) Với x ∈ (−1;1) ta có y' = 0 thì hàm số y không đổi.

Lời giải bài tập Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 12 Kết nối tri thức hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved.