Bài 9.43 trang 110 Toán 8 Tập 2 | Kết nối tri thức Giải Toán 8
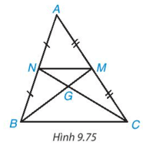
Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.
Giải Toán 8 Bài tập cuối chương 9 (trang 110, 111) - Kết nối tri thức
Bài 9.43 trang 110 Toán 8 Tập 2: Hai đường trung tuyến BM, CN của tam giác ABC cắt nhau tại điểm G (H.9.75). Chứng minh rằng tam giác GMN đồng dạng với tam giác GBC và tìm tỉ số đồng dạng.
Lời giải:
Vì BM, CN là các đường trung tuyến của tam giác ABC nên M, N lần lượt là trung điểm của AC, AB.
Suy ra MN là đường trung bình của tam giác ABC.
Do đó, MN // BC.
Suy ra (hai góc ở vị trí so le trong).
Mặt khác (hai góc đối đỉnh).
Do đó, ∆GMN ∽ ∆GBC (g.g).
Vì MN là đường trung bình của tam giác ABC nên BC = 2MN.
Khi đó, .
Vậy ∆GMN ∽ ∆GBC với tỉ số đồng dạng bằng .
Lời giải bài tập Toán 8 Bài tập cuối chương 9 (trang 110, 111) hay, chi tiết khác:
Bài 9.37 trang 110 Toán 8 Tập 2: Cho ABC là tam giác không cân ....
Bài 9.38 trang 110 Toán 8 Tập 2: Cho ΔA′B′C′ ∽ ΔABC với tỉ số đồng dạng ....
Bài 9.39 trang 110 Toán 8 Tập 2: Trong các bộ ba số đo dưới đây, đâu là số ....
Bài 9.40 trang 110 Toán 8 Tập 2: Cho tam giác ABC vuông tại A (AB ≠ AC) ....
Bài 9.42 trang 110 Toán 8 Tập 2: Cho Hình 9.74, biết rằng ....